# 数据结构：队列 Queue

作者：小傅哥
博客：https://bugstack.cn (opens new window)
原文：https://mp.weixin.qq.com/s/fpXGTjHeaYKULt3kqm1NTw (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

什么是队列？

在计算机科学中，队列(queue) 是一种特殊类型的抽象数据类型或集合（可以用链表实现，也可以用数组实现）。集合中的实体对象按顺序保存，可以通过在序列的一端添加实体和从序列的另一端移除实体来进行修改。

将元素添加到队列后的操作称为入队，从队列中移除元素的操作称为出队。也允许其他的一些操作，包括 peek、element等。另外队列还分为 单端队列(queue) 和 双端队列(deque) ，这在本章节要实现的优先队列中会有所体现。

# 二、队列数据结构

在计算机科学中, 一个 队列(queue) 是一种特殊类型的抽象数据类型或集合。集合中的实体按顺序保存。

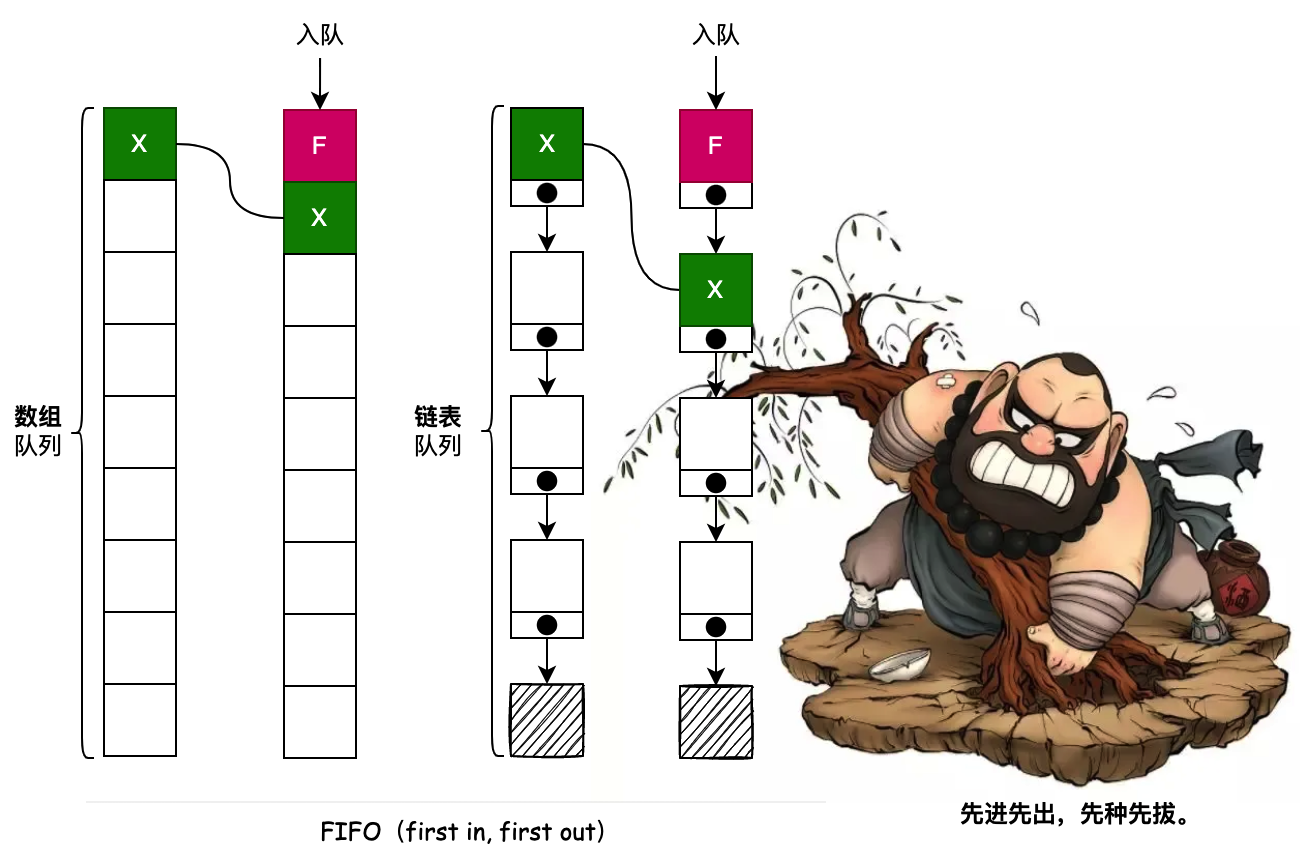
从理论上讲，队列的一个特征是它没有特定的容量。不管已经包含多少元素，总是可以再添加一个新元素。
队列既可以是数组实现也可以是链表实现。所以当我们在 Java 中使用队列的时候，Deque 的实现类就是；LinkedList 和 ArrayDeque的实现类。
队列不只是单端从一个口入另外一个口出，也可以是双端队列。例如在 Java 中 Queue 是单端队列接口、Deque 是双端队列接口，都有对应的实现类。

# 三、延迟队列介绍

队列的数据结构更像是数组和链表的变种，只要能看懂数组和链表，就能看懂队列。那么这里我们来扩展实现一个延迟队列，并在这个过程中会涉及到阻塞队列、优先队列的使用。通过这样的一个手写源码的学习队列的扩展使用。

本章节我们就借着数组结构的学习，实现一个延迟队列的 DelayQueue，让使用 Java 的读者既能了解学习数据结构，也能了解到 Java 源码实现。

源码地址：https://github.com/fuzhengwei/java-algorithms (opens new window) - Java 算法与数据结构
本章源码：https://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/queue (opens new window)

# 1. 延迟队列说明

DelayQueue 是一个 BlockingQueue（无界阻塞）队列，它封装了一个使用完全二叉堆排序元素的 PriorityQueue（优先队列）。在添加元素时使用 Delay（延迟时间）作为排序条件，延迟最小的元素会优先放到队首。

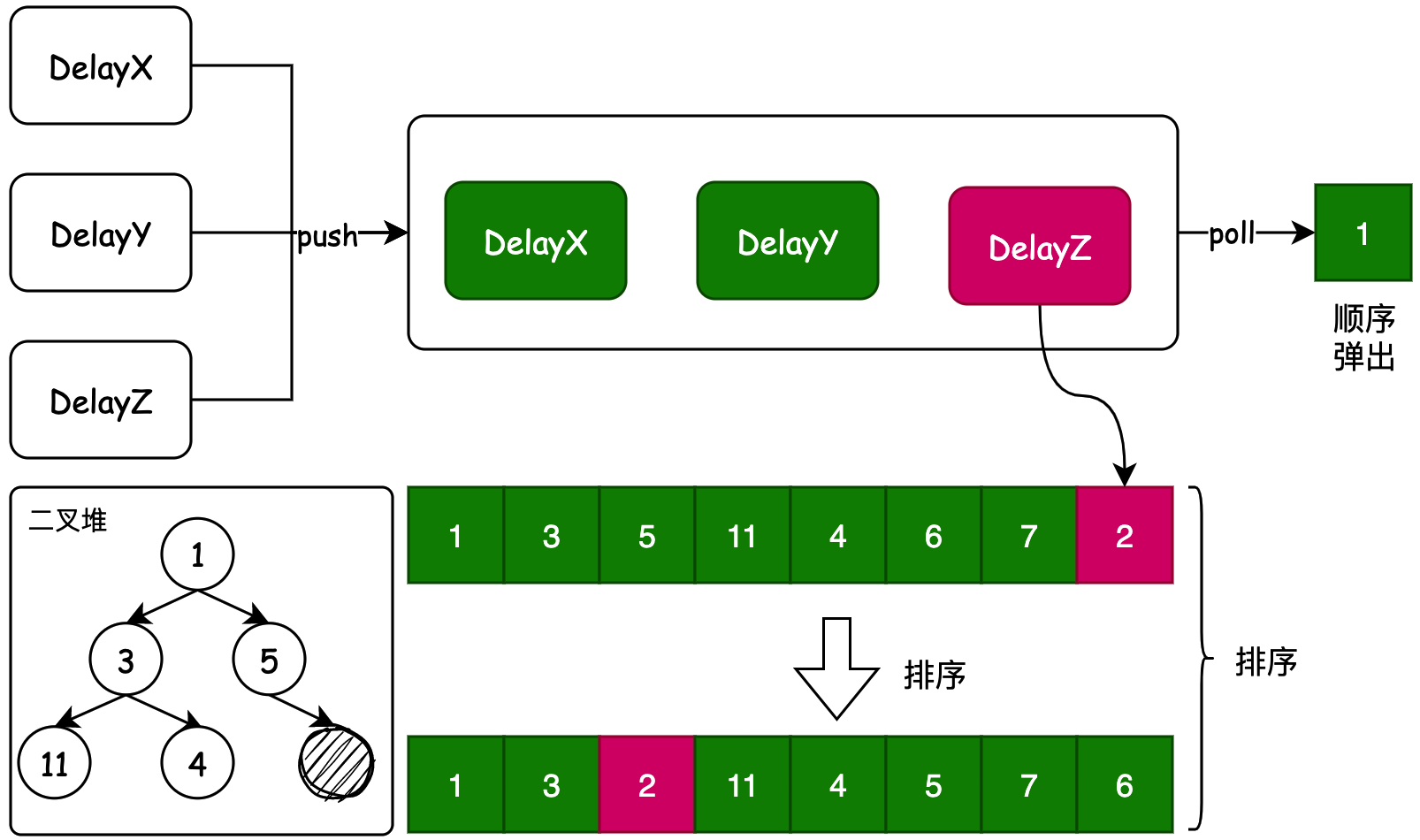
延迟队列的第一个核心点在于对所加入的元素按照一定的规则进行排序存放，这样才能让在延迟弹出元素的时候，按照所存放元素的排序进行输出。
那么这个延迟队列中用到的排序方式就是 PriorityQueue 优先队列，它的数据结构是数组实现的队列，但体现形式是一棵二叉堆树结构。在元素存放时，通过对存放元素的比较和替换形成二叉堆结构。

# 2. 二叉堆结构

二叉堆是一种特殊结构的堆，它的表现形态可以是一棵完整或近似二叉树的结构。如我们本章节要实现的延迟队列中的元素存放，使用的就是 PriorityQueue 实现的平衡二叉堆结构，数据以队列形式存放在基础数组中。

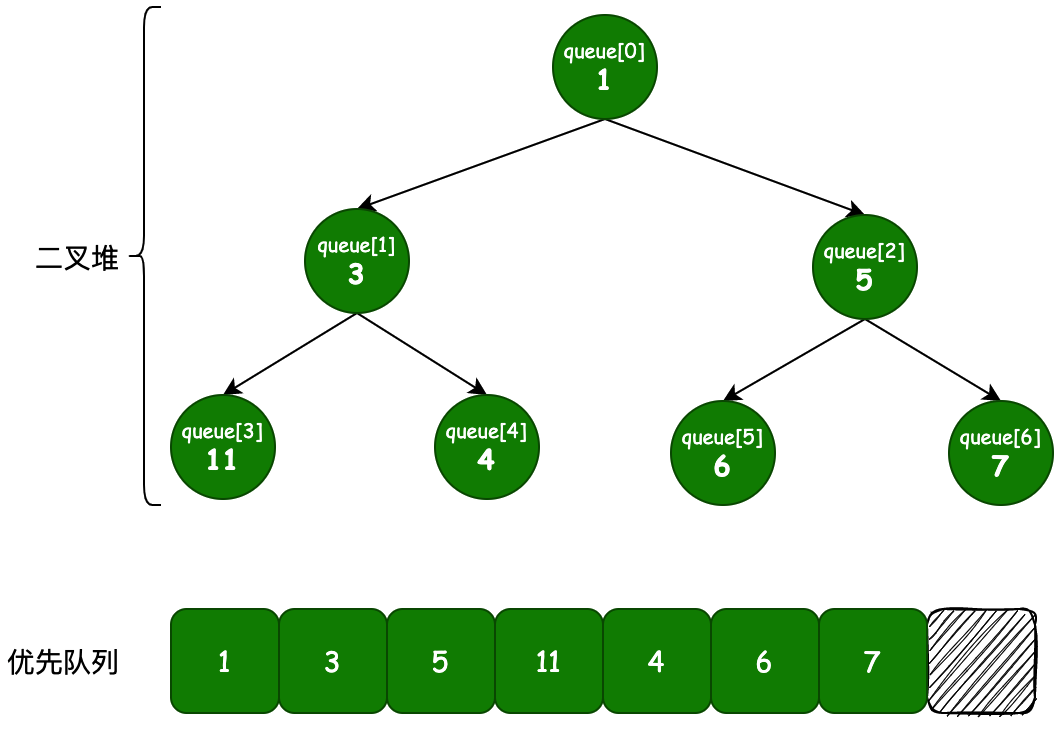
父子节点索引关系：
- 假如父节点为queue[n]，那么左子节点为queue[2n+1]，右子节点为queue[2n+2]
- 任意孩子节点的父节点位置，都是 (n-1)>>>1 相当于减1后除2取整
节点间大小关系：
- 父节点小于等于任意孩子节点
- 同一层级的两个孩子节点大小不需要维护，它是在弹出元素的时候进行判断的
子叶节点与非子叶节点：
- 一个长度为 size 的优先级队列，当 index >= size >>> 1 时，该节点为叶子节点。否则，为非叶子节点。

# 四. 延迟队列实现

# 1. 实现介绍

延迟队列的实现，主要为在优先队列的基础上，添加可重入锁 ReentrantLock 对阻塞队列的实现。当数据存放时，按照二叉堆结构排序元素，出队时依照排序结构进行迁移。

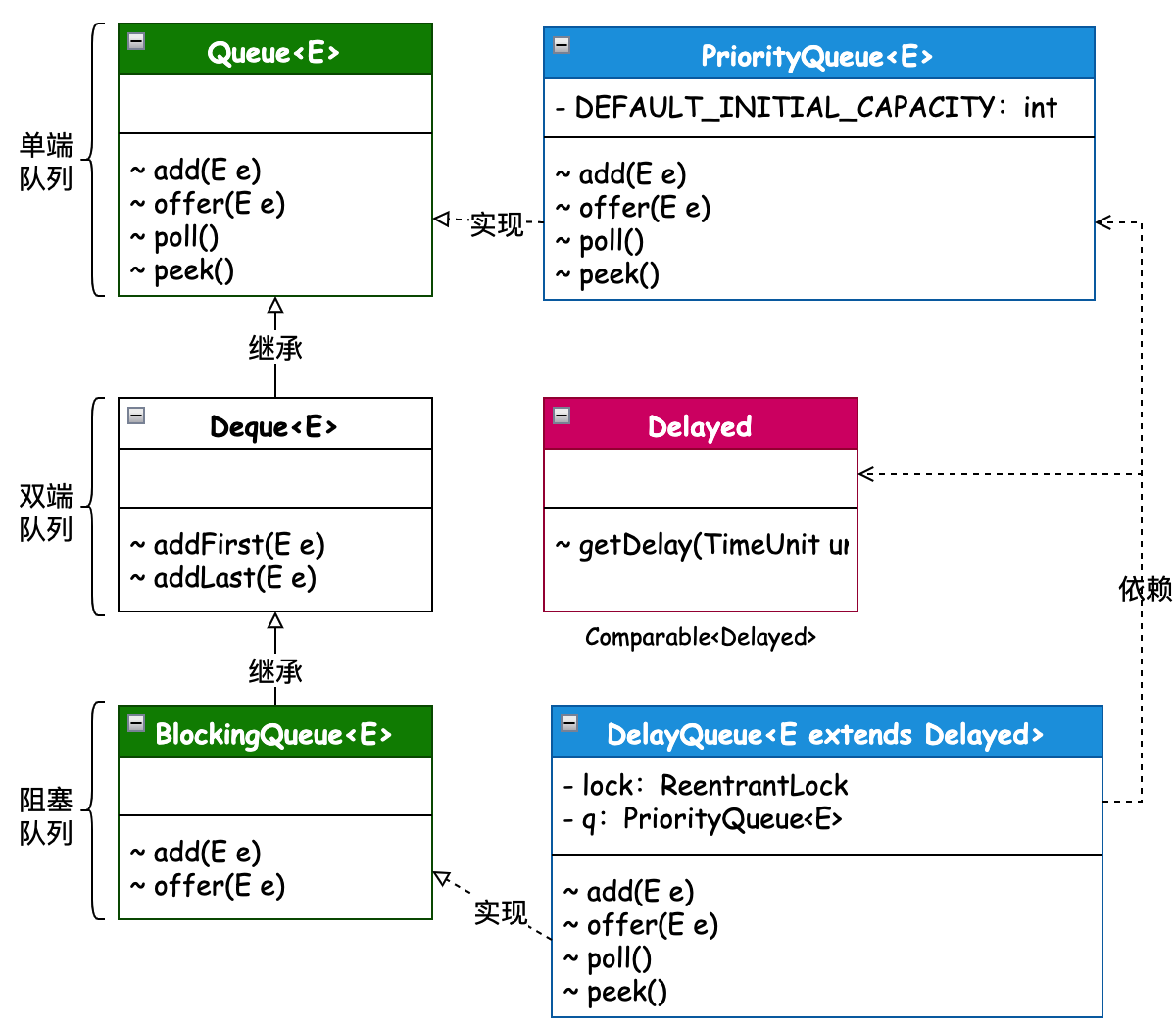
延迟队列的使用，是以在 DelayQueue 中存放实现了 Delayed 延迟接口的对象。因为只有实现这个对象，才能比较出当前元素与所需存放到对应位置的一个比对计算过程。
另外这里的核心点包括：PriorityQueue —— 优先队列、ReentrantLock —— 可重入锁、Condition —— 信号量

# 2. 入队实现

二叉堆的在存放元素时，以遵循它的特点，会在存存放过程中，通过队尾元素向上比对迁移。

private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        // 获取父节点Idx，相当于除以2
        int parent = (k - 1) >>> 1;
        logger.info("【入队】寻找当前节点的父节点位置。k：{} parent：{}", k, parent);
        Object e = queue[parent];
        // 如果当前位置元素大于父节点元素，则退出循环
        if (key.compareTo((E) e) >= 0) {
            logger.info("【入队】值比对，父节点：{} 目标节点：{}", JSON.toJSONString(e), JSON.toJSONString(key));
            break;
        }
        // 相反当前位置元素小于父节点位置，则进行替换
        logger.info("【入队】替换过程，父子节点位置替换，继续循环。父节点值：{} 存放到位置：{}", JSON.toJSONString(e), k);
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
    logger.info("【入队】完成 Idx：{} Val：{} \r\n当前队列：{} \r\n", k, JSON.toJSONString(key), JSON.toJSONString(queue));
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

DelayQueue 延迟队列，元素入队最终会调用到优先队列的 PriorityQueue#siftUpComparable 方法。
以入队元素2举例，如图所示入队过程。
(k - 1) >>> 1 为什么使用 >>> 右移1位；
- 首先我们是需要通过右移替代除以2的运算，提升运算效率，找到父节点。移位器比除法器简单得多，在大多数处理器上，移位指令的执行速度比除法指令快
- >> 是算术位移，>>> 是逻辑右移
- 算术和逻辑左移和乘法的等价，但由于符号位的存在算术右移和除法不等价。wiki：算术移位 (opens new window)、逻辑移位 (opens new window)

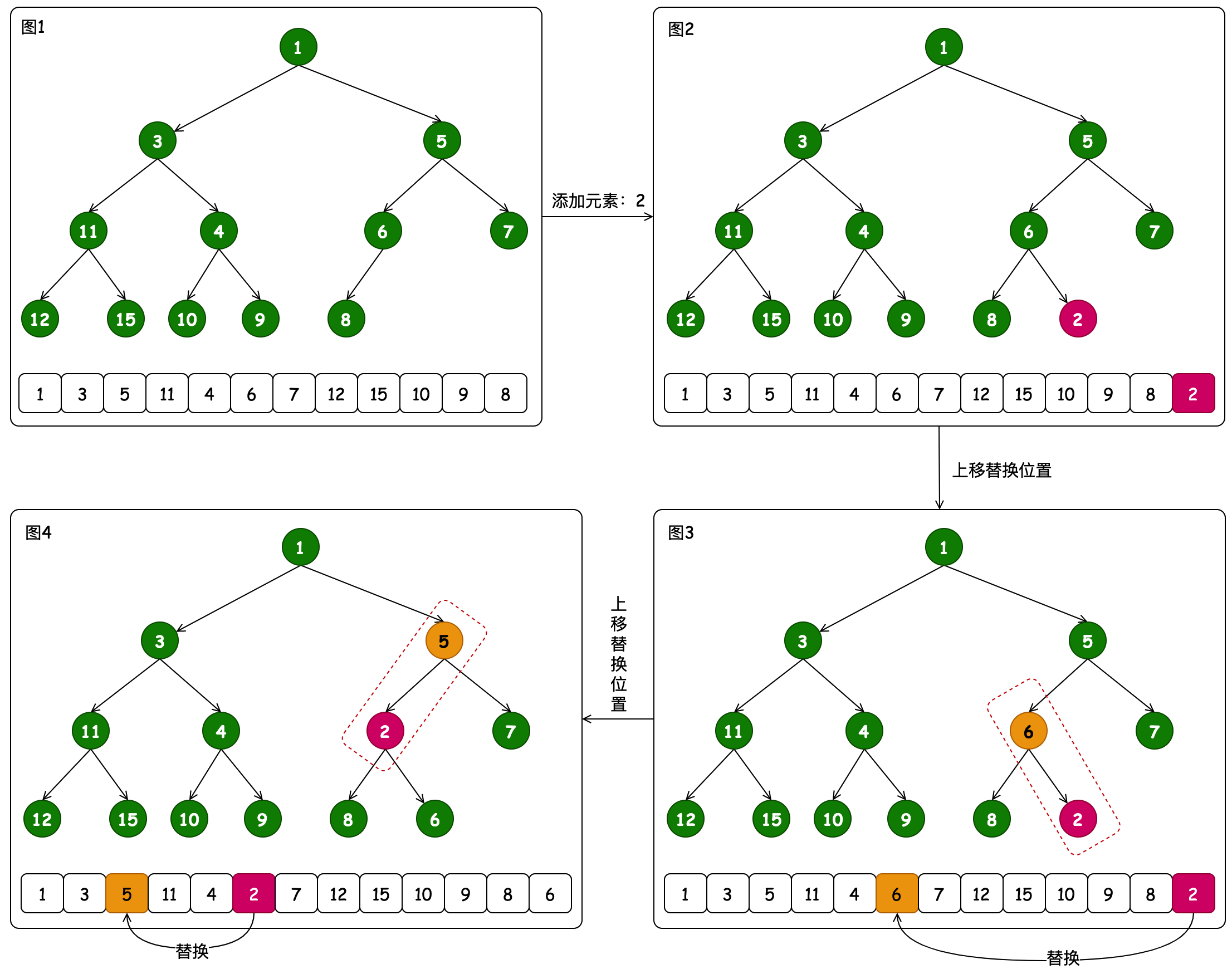
首先将元素2挂到队列尾部，之后通过 (k - 1) >>> 1 计算父节点位置，与对应元素进行比对和判断交换。
交换过程包括2->6、2->5，以此交换结束后元素保存完毕。

单元测试

Queue<Job> queue = new DelayQueue<>();
queue.add(new Job("1号", 1000L));
queue.add(new Job("3号", 3000L));
queue.add(new Job("5号", 5000L));
queue.add(new Job("11号", 11000L));
queue.add(new Job("4号", 4000L));
queue.add(new Job("6号", 6000L));
queue.add(new Job("7号", 7000L));
queue.add(new Job("12号", 12000L));
queue.add(new Job("15号", 15000L));
queue.add(new Job("10号", 10000L));
queue.add(new Job("9号", 9000L));
queue.add(new Job("8号", 8000L));
// 新增入队
queue.add(new Job("2号", 2000L));

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

测试结果

【入队】元素：{"name":"2号"} 当前队列：[{"name":"1号"},{"name":"3号"},{"name":"5号"},{"name":"11号"},{"name":"4号"},{"name":"6号"},{"name":"7号"},{"name":"12号"},{"name":"15号"},{"name":"10号"},{"name":"9号"},{"name":"8号"},null,null,null,null,null,null,null,null,null,null,null,null]
【入队】寻找当前节点的父节点位置。k：12 parent：5
【入队】替换过程，父子节点位置替换，继续循环。父节点值：{"name":"6号"} 存放到位置：12
【入队】寻找当前节点的父节点位置。k：5 parent：2
【入队】替换过程，父子节点位置替换，继续循环。父节点值：{"name":"5号"} 存放到位置：5
【入队】寻找当前节点的父节点位置。k：2 parent：0
【入队】值比对，父节点：{"name":"1号"} 目标节点：{"name":"2号"}
【入队】完成 Idx：2 Val：{"name":"2号"} 
当前队列：[{"name":"1号"},{"name":"3号"},{"name":"2号"},{"name":"11号"},{"name":"4号"},{"name":"5号"},{"name":"7号"},{"name":"12号"},{"name":"15号"},{"name":"10号"},{"name":"9号"},{"name":"8号"},{"name":"6号"},null,null,null,null,null,null,null,null,null,null,null]

1
2
3
4
5
6
7
8
9

通过打印结果可以看到，2号元素入队时候队列的情况，以及从入队开始寻找父节点，并进行值的比对和上异操作。直至结果比对完成把2号元素存入对应的位置。

# 3. 出队实现

元素的出队其实很简单，只要把根元素直接删除弹出即可。但剩余接下里的步骤才是复杂的，因为需要在根元素迁移走后，寻找另外的最小元素迁移到对头。这个过程与入队正好相反，这是一个不断向下迁移的过程。

private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    // 先找出中间件节点
    int half = size >>> 1;
    while (k < half) {
        // 找到左子节点和右子节点，两个节点进行比较，找出最大的值
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        // 左子节点与右子节点比较，取最小的节点
        if (right < size && ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0) {
            logger.info("【出队】左右子节点比对，获取最小值。left：{} right：{}", JSON.toJSONString(c), JSON.toJSONString(queue[right]));
            c = queue[child = right];
        }
        // 目标值与c比较，当目标值小于c值，退出循环。说明此时目标值所在位置适合，迁移完成。
        if (key.compareTo((E) c) <= 0) {
            break;
        }
        // 目标值大于c值，位置替换，继续比较
        logger.info("【出队】替换过程，节点的值比对。上节点：{} 下节点：{} 位置替换", JSON.toJSONString(queue[k]), JSON.toJSONString(c));
        queue[k] = c;
        k = child;
    }
    // 把目标值放到对应位置
    logger.info("【出队】替换结果，最终更换位置。Idx：{} Val：{}", k, JSON.toJSONString(key));
    queue[k] = key;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

DelayQueue 延迟队列，元素出队会调用到 PriorityQueue#siftDownComparable 方法，不断地向下迁移元素。这个过程会比对左右子节点的值，找到最小的。所以整个过程会比入队麻烦一些。

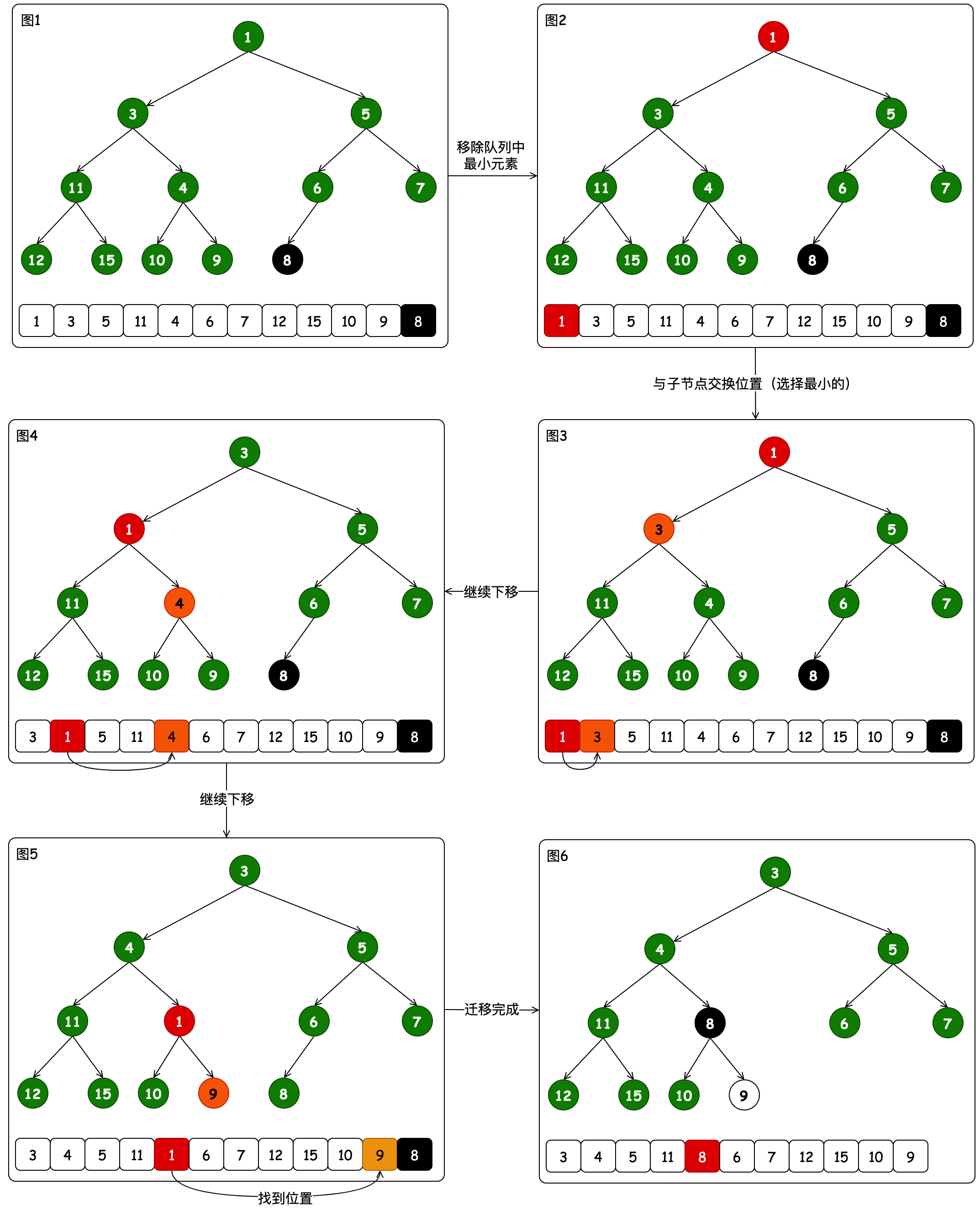
这里以弹出元素1举例，之后将队尾元素替换到相应的位置。整个过程分为6张图表述。

图1到图2，找出根元素弹出。
图3到图4，将根元素向下迁移，与子元素比对，并替换位置。如果这个位置与8相比，小于8则继续向下迁移。
图4到图5，继续迁移，在原节点4的位置对应的两个子元素，都比8大，这个时候就可以停下来了。
图5到图6，更换元素位置，把队尾的元素替换到对应元素1向下迁移检测的位置。

单元测试

@Test
public void test_queue() throws InterruptedException {
    Queue<Job> queue = new DelayQueue<>();
    queue.add(new Job("1号", 1000L));
    queue.add(new Job("3号", 3000L));
    queue.add(new Job("5号", 5000L));
    queue.add(new Job("11号", 11000L));
    queue.add(new Job("4号", 4000L));
    queue.add(new Job("6号", 6000L));
    queue.add(new Job("7号", 7000L));
    queue.add(new Job("12号", 12000L));
    queue.add(new Job("15号", 15000L));
    queue.add(new Job("10号", 10000L));
    queue.add(new Job("9号", 9000L));
    queue.add(new Job("8号", 8000L));
    
    while (true) {
        Job poll = queue.poll();
        if (null == poll) {
            Thread.sleep(10);
            continue;
        }
        System.out.println(poll.getName());
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

测试结果

16:20:26.273 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：{"name":"1号"} 下节点：{"name":"3号"} 位置替换
16:20:26.273 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】左右子节点比对，获取最小值。left：{"name":"11号"} right：{"name":"4号"}
16:20:26.273 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：{"name":"3号"} 下节点：{"name":"4号"} 位置替换
16:20:26.273 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】左右子节点比对，获取最小值。left：{"name":"10号"} right：{"name":"9号"}
16:20:26.273 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：4 Val：{"name":"8号"}
1号
16:20:28.272 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：{"name":"3号"} 下节点：{"name":"4号"} 位置替换
16:20:28.272 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】左右子节点比对，获取最小值。left：{"name":"11号"} right：{"name":"8号"}
16:20:28.272 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：{"name":"4号"} 下节点：{"name":"8号"} 位置替换
16:20:28.272 [main] INFO cn.bugstack.algorithms.data.queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：4 Val：{"name":"9号"}
3号
...

1
2
3
4
5
6
7
8
9
10
11
12

举例1号、3号元素的出队过程。每个元素的出队，都会进行元素的位置迁移操作，整个过程也都如上图所示一样。

# 4. 操作加锁

在延迟队列关于元素的操作中，都会进行加锁处理。

offer：——入队元素

public boolean offer(E e) {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        q.offer(e);
        if (q.peek() == e) {
            available.signal();
        }
        return true;
    } finally {
        lock.unlock();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

poll：——出队元素

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        E first = q.peek();
        if (first == null || first.getDelay(NANOSECONDS) > 0) {
            return null;
        } else {
            return q.poll();
        }
    } finally {
        lock.unlock();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

元素的入队和出队都会使用 ReentrantLock 的方式进行加锁处理。确保线程安全。

# 五、常见面试问题

单端队列和双端队列，分别对应的实现类是哪个？
简述延迟队列/优先队列的实现方式
二叉堆插入/弹出元素的过程
延迟队列的使用场景
延迟队列为什么添加信号量

← 数组 Array 堆栈（栈）Stack →

常用搜索	百度 Google Bing Github 搜代码
技术社区	CDSN 博客园 OSChina 思否掘金 Linux公社 IBM 开发者 StackOverflow
PDF 下载	《Java 面经手册》《重学Java设计模式》《手撸 Spring》《字节码编程》
面试求职	简历优化简历筛选大厂要求薪资待遇北漂生活
Java相关	数据结构和算法并发和锁多线程 Java8 特性 JVM 虚拟机
Spring	手写 Spring SpringCloud 入门 Mybatis 源码分析手写 Mybatis Quartz 源码分析
面向对象	设计模式 DDD 落地低代码字节码插桩画架构图系统监控中台研发规范
中间件&插件	Maven中央仓库数据库路由设计 IDEA-Plugin
Netty 4.x	基础入门中级拓展高级应用 RPC 实现 IM 仿微信
字节码编程	ASM Javassist Byte-Buddy JavaAgent ASM-DOC JVM 指令码
专栏小册	《Netty+JavaFx实战：仿桌面版微信聊天》《SpringBoot 中间件设计和开发》《Lottery 抽奖系统 - 基于领域驱动设计的四层架构实践》
知识星球	码农会锁实战项目