# 数据结构：红黑树 Red Black Tree

作者：小傅哥
博客：https://bugstack.cn (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

红黑树的历史

红黑树（Red Black Tree）是一种自平衡二叉查找树，于 1972 年由 Rudolf Bayer 发明的对称二叉B树演化而来，并以2-3-4树、2-3树流行。最终在 1978 年由 Leonidas J. Guibas 和 Robert Sedgewick 从对称二叉 B 树中推导出红黑树。PS：之所以选择“红色”，是因为它是作者在Xerox PARC工作时可用的彩色激光打印机产生的最好看的颜色。

# 二、红黑树数据结构

建立在 BST 二叉搜索树的基础上，AVL、2-3树、红黑树都是自平衡二叉树（统称B-树）。但相比于AVL树，高度平衡所带来的时间复杂度，红黑树对平衡的控制要宽松一些，红黑树只需要保证黑色节点平衡即可。也正因红黑树在插入和删除时不需要太多的平衡操作，也让它成为；Java中HashMap的元素碰撞后的转换、Linux的CFS进行调度算法、多路复用技术的Epoll等各类底层的数据结构实现。

但红黑树并不是一个那么容易理解的知识点，甚至很多资料都只是给出红黑树的理论，但为什么要染色、为什么要左旋、为什么还要左旋接右旋。这样的知识点本就不应该是考死记硬背来学习的，这根本不是学习编程的”套路“。—— 你背的再溜，也没法理解核心本质，忘也只是时间的问题！

其实根据红黑树的历史来看，最早红黑树就是来自于2-3树的结构，所以要学习清楚的结构就要学习 2-3树。但同时对于 2-3树的学习也不能只是依靠一份理论，否则对于红黑的学习来看，就是用不太理解的 2-3树理论套红黑树理论，依旧没法理解。所以小傅哥在上一章专门讲解了 2-3树，并做了具体的代码实现。

现在来本章，我们在来看看红黑树与2-3树的关系；

红黑树	红黑树	2-3树

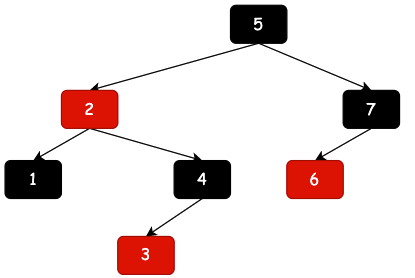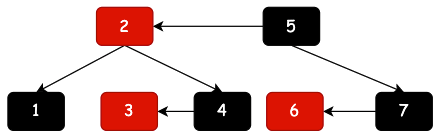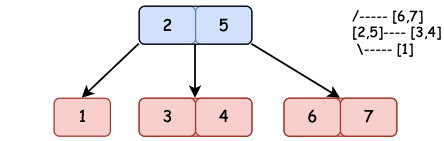一棵标准二叉红黑树	红黑树演化（红色节点拉平）	最终恢复到2-3树

红黑树一棵在2-3树基础上的左倾红黑树，这样就可以把红色节点与对应的父节点拉平，再把两个拉平的节点放到一个节点中。就是我们熟悉的2-3树了。如果你还没有学习过2-3树，最好先看下小傅哥的2-3树，否则你会看的很吃力

现在再来看下红黑树的五条定义；

每个节点不是红色就是黑色。
- 黑色决定平衡，红色不决定平衡。这对应了2-3树中一个节点内可以存放1~2个节点。
根是黑色的。
- 这条规则有时会被省略。由于根总是可以从红色变为黑色，但不一定相反，因此该规则对分析几乎没有影响。
所有叶子 (NIL) 都是黑色的。
- 这里指的是红黑树都会有一个空的叶子节点，是红黑树自己的规则。
如果一个节点是红色的，那么它的两个子节点都是黑色的。
- 通常这条规则也叫不会有连续的红色节点。这体现在2-3树中，一个节点最多临时会有3个节点，中间是黑色节点，左右是红色节点。2-3树中出现这样的情况后，会进行节点迁移，中间节点成为父节点，左右节点成为子节点。
从给定节点到其任何后代 NIL 节点的每条路径都包含相同数量的黑色节点。
- 对应2-3树中，每一层都只是有一个节点贡献了树高决定平衡性，也就是对应红黑树中的黑色节点。

好啦，现在再看这5条理论是不就不需要再死记硬背了。因为编程本就是对数学逻辑的具体实现，只要把核心逻辑理顺其实很好理解。接下来小傅哥就带着大家动手实现一下红黑树。

# 三、红黑树结构实现

基于 BST 二叉搜索树的基础上，AVL树添加了树高作为计算平衡因子的条件，那么红黑树也需要添加一个新的颜色属性，用于处理平衡操作。

public class Node {

    public Class<?> clazz;
    public Integer value;
    public Node parent;
    public Node left;
    public Node right;

    // AVL 树所需属性
    public int height;
    // 红黑树所需属性
    public Color color = Color.RED;
    
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

相比于AVL树通过左右旋转平衡树高，红黑树则是在2-3树的基础上，只对黑色节点维护树高，所以它会使用到染色和左右旋来对树高调衡。染色与左右旋相比，减少了平衡操作

源码地址：https://github.com/fuzhengwei/java-algorithms (opens new window)
本章源码：https://github.com/fuzhengwei/java-algorithms/tree/main/data-structures/src/main/java/tree (opens new window)
动画演示：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html (opens new window)—— 红黑树初次理解还是比较困难的，可以结合学习内容的同时做一些动画演示。

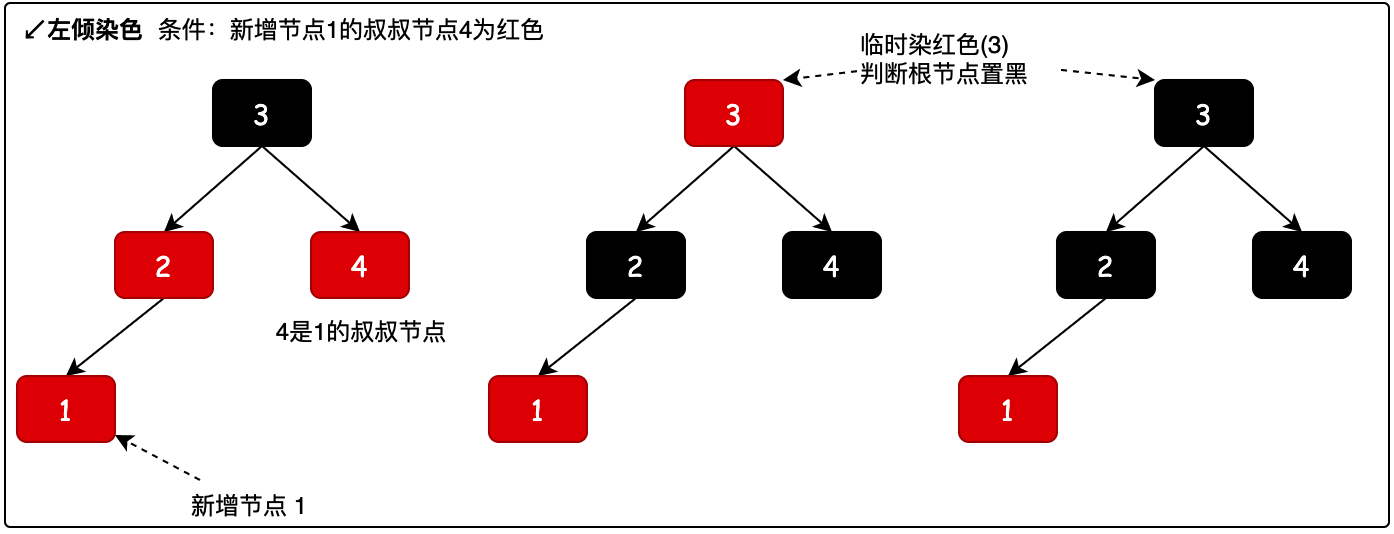
# 1. 左倾染色

新增节点1，相当于2-3树中在节点2上添加了一个节点，这个时候并不影响树高，只需要染色保持红黑树的规则即可。染色过程如图所示。

Node uncle = grandParent.right;
// 染色
if (uncle.color == Node.Color.RED){
    parent.color = Node.Color.BLACK;
    uncle.color = Node.Color.BLACK;
    grandParent.color = Node.Color.RED;
    current = grandParent;
}

1
2
3
4
5
6
7
8

染色时根据当前节点的爷爷节点，找到当前节点的叔叔节点。
再把父节点染黑、叔叔节点染黑，爷爷节点染红。但爷爷节点染红是临时的，当平衡树高操作后会把根节点染黑。具体参考源码

# 2. 右倾染色

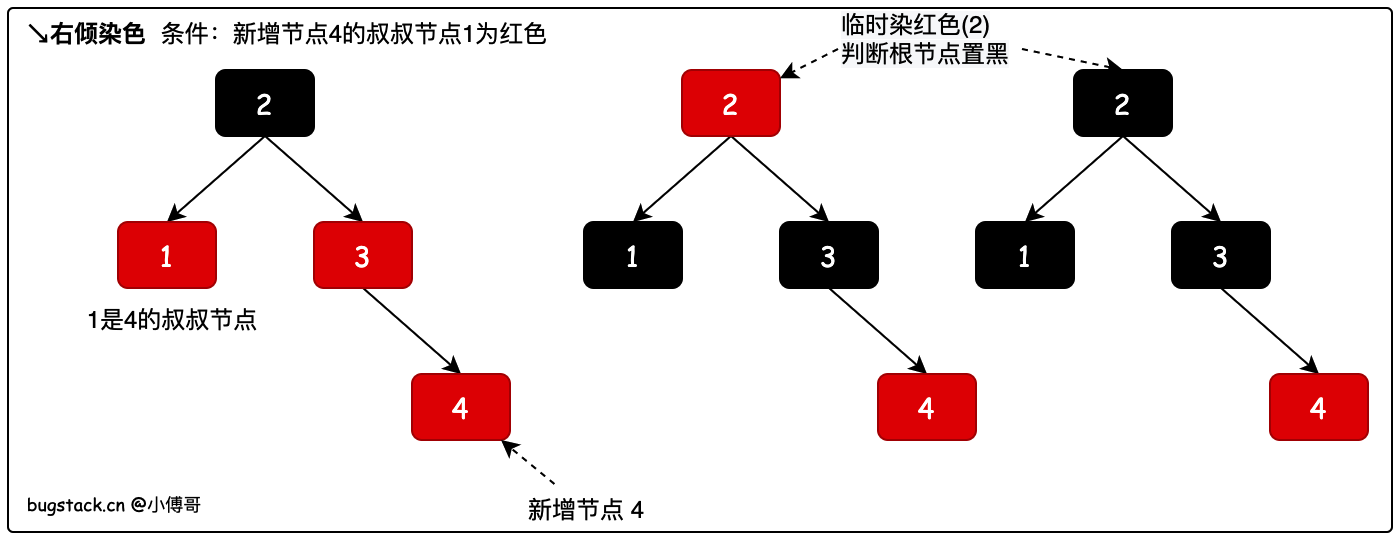
新增节点4，相当于2-3树中在节点3上添加了一个节点，这个时候并不影响树高，只需要染色保持红黑树的规则即可。染色过程如图所示。

Node uncle = grandParent.left;
// 染色
if(uncle.color == Node.Color.RED){
    parent.color = Node.Color.BLACK;
    uncle.color = Node.Color.BLACK;
    grandParent.color = Node.Color.RED;
    current= grandParent;
}

1
2
3
4
5
6
7
8

染色时根据当前节点的爷爷节点，找到当前节点的叔叔节点。
再把父节点染黑、叔叔节点染黑，爷爷节点染红。但爷爷节点染红是临时的，当平衡树高操作后会把根节点染黑。具体参考源码

# 3. 左旋调衡

# 3.1 一次左旋

对照2-3树，只有当一个节点内有3个节点的时候，才需要调衡。那么红黑树则是判断当前节点的叔叔节点是否为红色节点，如果不是则没法通过染色调衡，也就是需要选择进行调衡。

parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateLeft(grandParent);

1
2
3

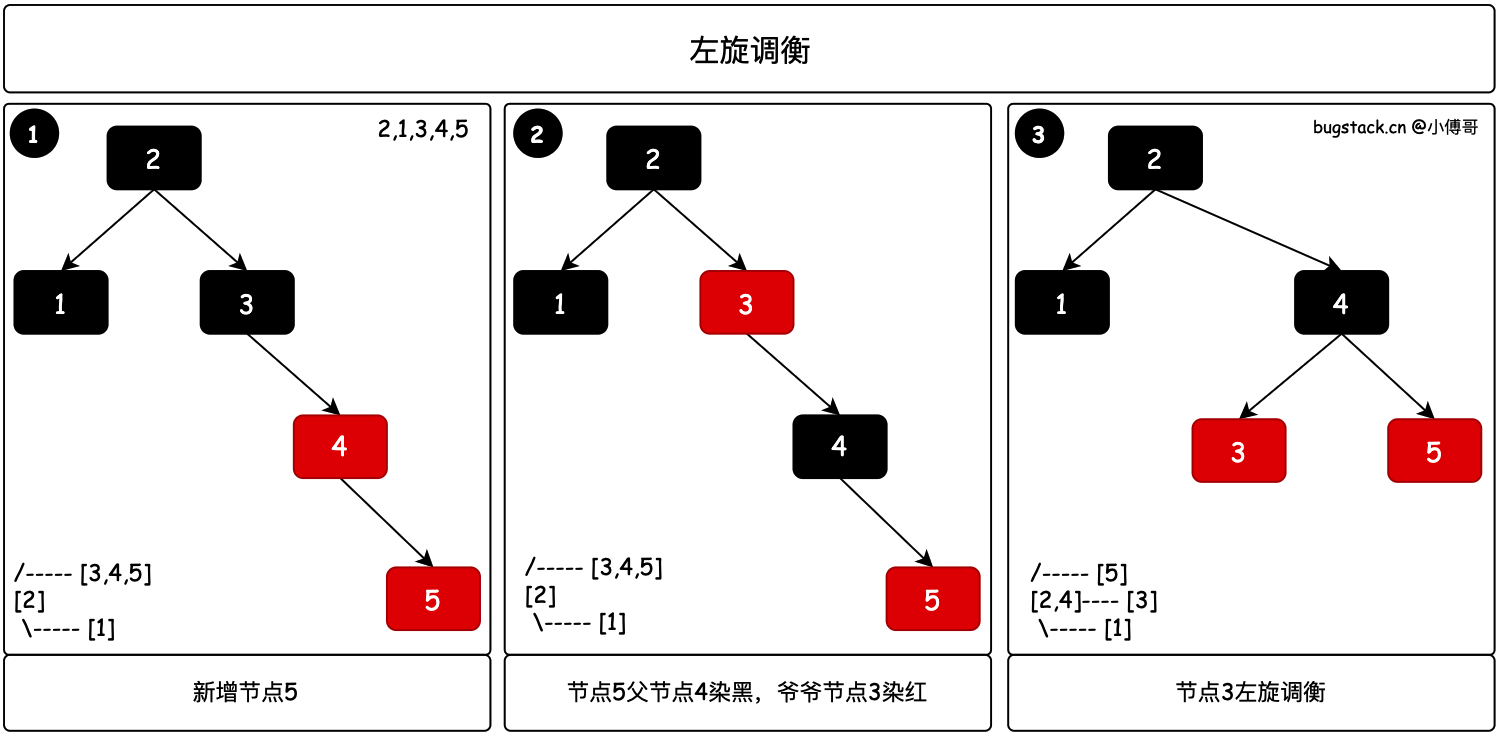
当你把红黑树对照理解成2-3树，如图中第1步骤下的左侧小图，新增的节点5导致2-3树不平衡。
那么这个时候需要把2-3树中节点4提起来，而对应红黑树则需要先进行染色，待操作的节点4为黑色，两个孩子节点为红色。
最后是把节点3进行一次左旋操作，完成树的平衡。对应步骤3中的左侧小图是2-3树调衡后的结果。

# 3.2 右旋 + 左旋

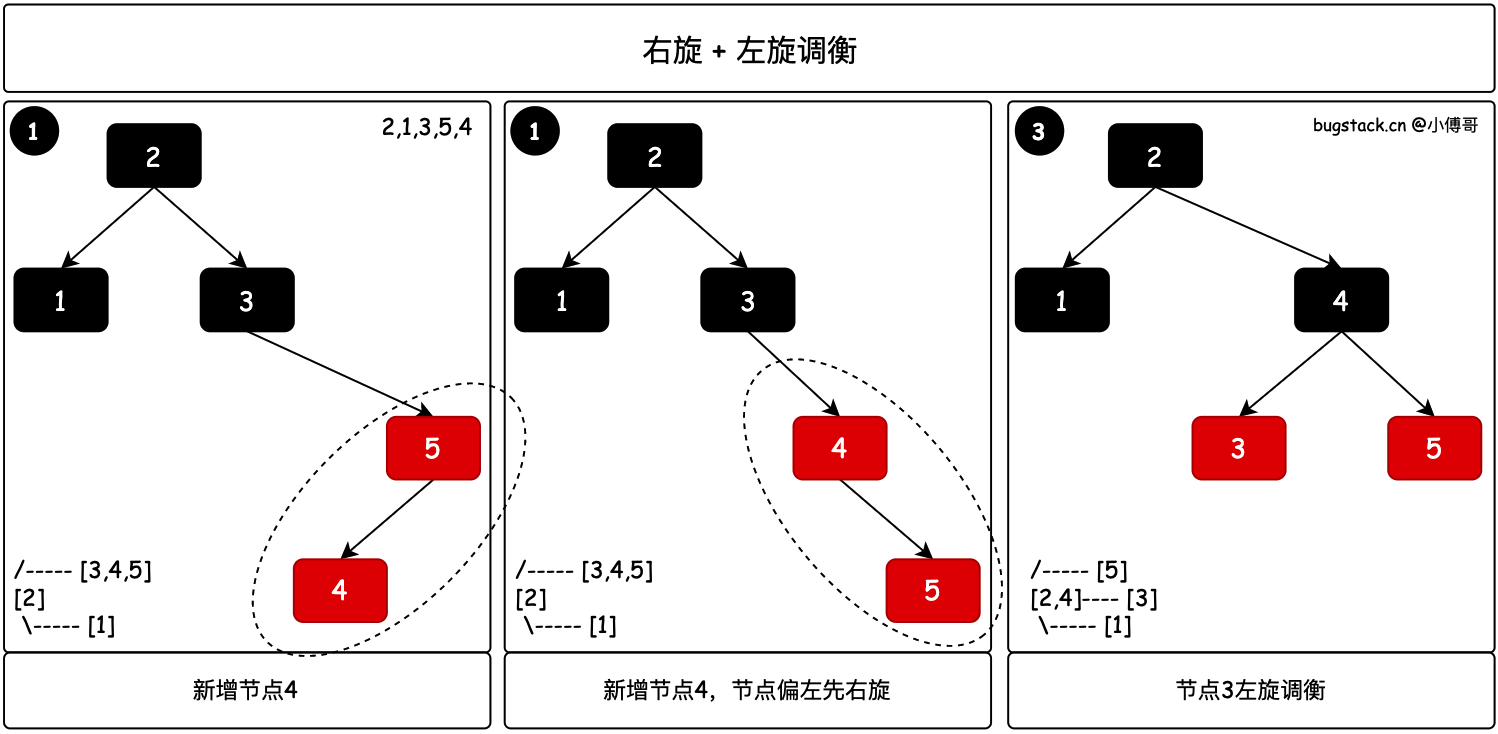
当一次左旋没法调衡，需要右旋+左旋的情况，在AVL树中有同样的场景。本身树需要左旋操作，但整体分支树节点偏左，此时需要右旋调整树结构再左旋。此处可参考小傅哥编写的AVL树 (opens new window)

// 偏左↙，先右旋一次调衡
if (current == parent.left){
    current = parent;
    super.rotateRight(current);
    parent = current.parent;
}
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateLeft(grandParent);

1
2
3
4
5
6
7
8
9

红黑树新增节点4以后，4↙5 结构偏左，需要先进行右旋调衡树结构，再进行左旋。其实这个时候再进行的左旋就和上面一次左旋操作一致了。

# 4. 右旋调衡

# 4.1 一次右旋

parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateRight(grandParent);

1
2
3

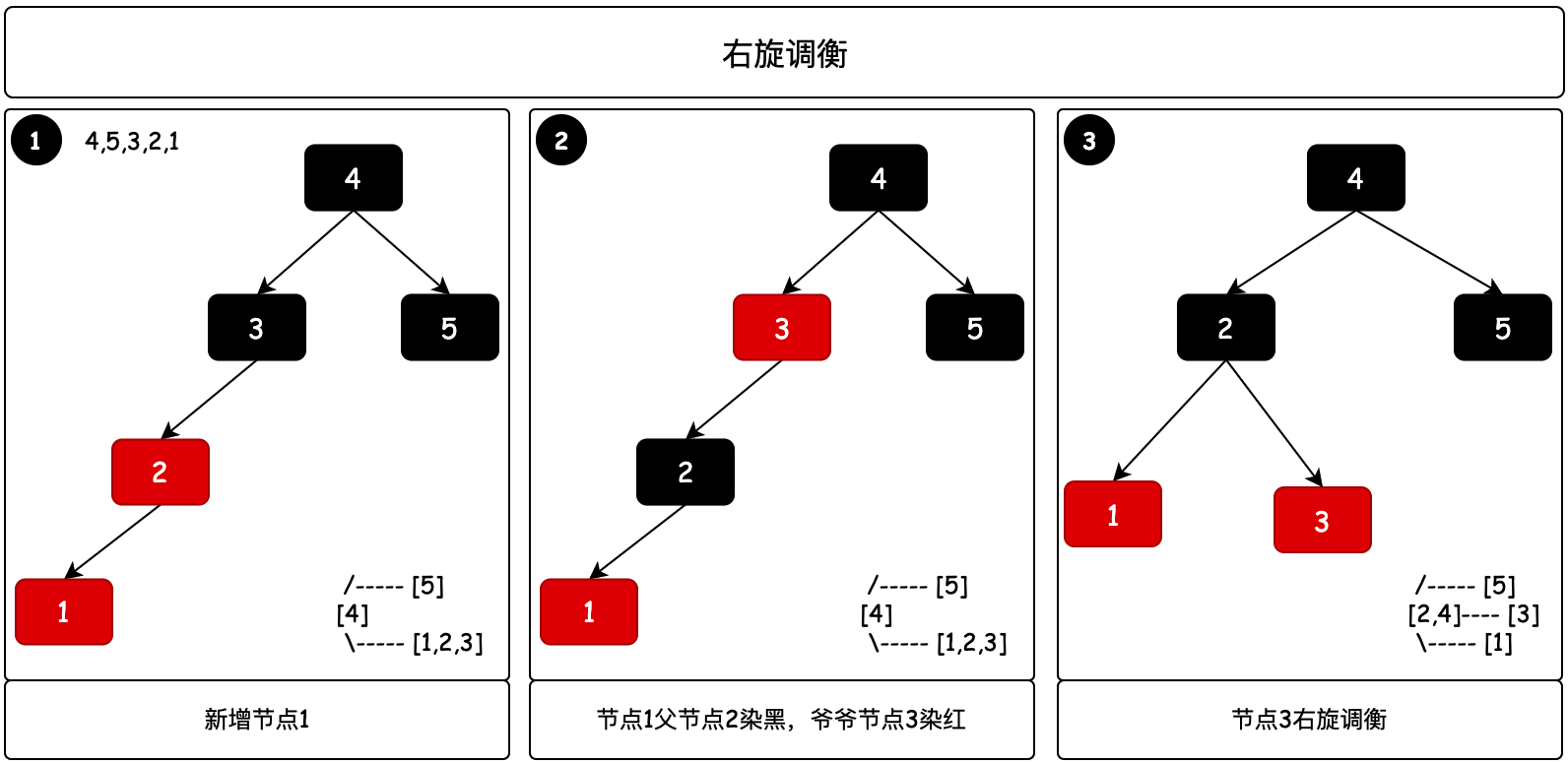
当你把红黑树对照理解成2-3树，如图中第1步骤下的右侧小图，新增的节点1导致2-3树不平衡。
那么这个时候需要把2-3树中节点2提起来，而对应红黑树则需要先进行染色，待操作的节点2为黑色，两个孩子节点为红色。
最后是把节点2进行一次右旋操作，完成树的平衡。对应步骤3中的右侧小图是2-3树调衡后的结果。

# 4.2 左旋 + 右旋

当一次左旋没法调衡，需要左旋+右旋的情况，在AVL树中有同样的场景。本身树需要右旋操作，但整体分支树节点偏右，此时需要左旋调整树结构再右旋。

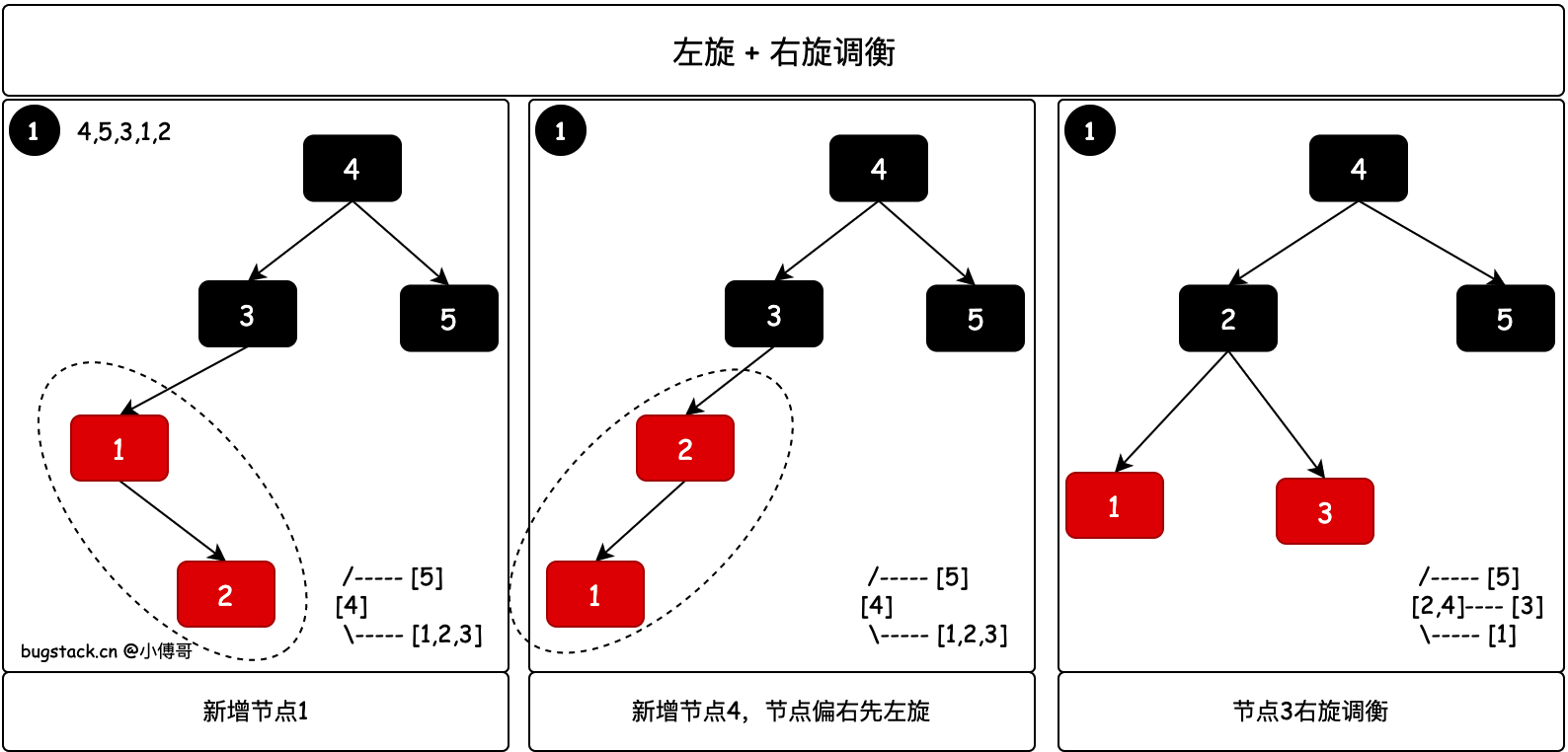
// 偏右↘，先左旋一次调衡
if (current == parent.right){
    current = parent;
    super.rotateLeft(current);
    parent = current.parent;
}
parent.color = Node.Color.BLACK;
grandParent.color = Node.Color.RED;
super.rotateRight(grandParent);

1
2
3
4
5
6
7
8
9

红黑树新增节点2以后，1↘2 结构偏右，需要先进行左旋调衡树结构，再进行右旋。其实这个时候再进行的右旋就和上面一次右旋操作一致了。

# 四、红黑树实现测试

为了验证红黑树的实现正确与否，这里我们做一下随机节点的插入，如果它能一直保持平衡，那么它就是一颗可靠红黑平衡树。

@Test
public void test_binary_search_tree() {
    Tree tree = new RedBlackTree();
    for (int i = 0; i < 20; i++) {
        tree.insert(new Random().nextInt(100));
    }
    System.out.println(tree);
}

1
2
3
4
5
6
7
8

测试结果

RedBlackTree，输入节点：79,92,36,35,72,22,11,66,98,28,30,39,56,26,1,25,33,80,22,23

                         /----- <NIL>
                 /----- 98(红)
                 |       \----- <NIL>
         /----- 92(黑)
         |       |       /----- <NIL>
         |       \----- 80(红)
         |               \----- <NIL>
 /----- 79(黑)
 |       |               /----- <NIL>
 |       |       /----- 72(黑)
 |       |       |       \----- <NIL>
 |       \----- 66(红)
 |               |               /----- <NIL>
 |               |       /----- 56(红)
 |               |       |       \----- <NIL>
 |               \----- 39(黑)
 |                       \----- <NIL>
36(黑)
 |                       /----- <NIL>
 |               /----- 35(黑)
 |               |       |       /----- <NIL>
 |               |       \----- 33(红)
 |               |               \----- <NIL>
 |       /----- 30(红)
 |       |       |       /----- <NIL>
 |       |       \----- 28(黑)
 |       |               \----- <NIL>
 \----- 26(黑)
         |                       /----- <NIL>
         |               /----- 25(红)
         |               |       \----- <NIL>
         |       /----- 23(黑)
         |       |       |       /----- <NIL>
         |       |       \----- 22(红)
         |       |               \----- <NIL>
         \----- 22(红)
                 |       /----- <NIL>
                 \----- 11(黑)
                         |       /----- <NIL>
                         \----- 1(红)
                                 \----- <NIL>

对照2-3树结构
                 /----- [98]
         /----- [92]
         |       \----- [80]
 /----- [79]
 |       |       /----- [72]
 |       \----- [66]
 |               \----- [39,56]
[36]
 |               /----- [33,35]
 |       /----- [30]
 |       |       \----- [28]
 \----- [26]
         |       
         |       /----- [25]
         \----- [22,23]----- [22]
                 \----- [1,11]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

随机插入20个节点，每个节点的顺序已经打印，经过红黑树的染色和左右旋调衡后，二叉结构始终保持树保持平衡，那么验证通过。
另外本文出现的案例已经在单元测试中都有编写，读者可以在源码中进行测试。

# 五、常见面试题

红黑树都有哪些使用场景？
相比于BST树，红黑树有什么用途？
B-树是什么意思，都包括哪些？
新增加一个节点后，什么情况下需要染色、什么情况要左旋、什么情况要左旋+右旋？
红黑树的特点是什么？

← 2-3树并查集 Disjoint-Set →

常用搜索	百度 Google Bing Github 搜代码
技术社区	CDSN 博客园 OSChina 思否掘金 Linux公社 IBM 开发者 StackOverflow
PDF 下载	《Java 面经手册》《重学Java设计模式》《手撸 Spring》《字节码编程》
面试求职	简历优化简历筛选大厂要求薪资待遇北漂生活
Java相关	数据结构和算法并发和锁多线程 Java8 特性 JVM 虚拟机
Spring	手写 Spring SpringCloud 入门 Mybatis 源码分析手写 Mybatis Quartz 源码分析
面向对象	设计模式 DDD 落地低代码字节码插桩画架构图系统监控中台研发规范
中间件&插件	Maven中央仓库数据库路由设计 IDEA-Plugin
Netty 4.x	基础入门中级拓展高级应用 RPC 实现 IM 仿微信
字节码编程	ASM Javassist Byte-Buddy JavaAgent ASM-DOC JVM 指令码
专栏小册	《Netty+JavaFx实战：仿桌面版微信聊天》《SpringBoot 中间件设计和开发》《Lottery 抽奖系统 - 基于领域驱动设计的四层架构实践》
知识星球	码农会锁实战项目