小傅哥 bugstack 虫洞栈

# 数据结构：2-3树

作者：小傅哥
博客：https://bugstack.cn (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

不讲红黑树，先讲2-3树里呢？

原本是想AVL树 (opens new window)讲解了左旋、右旋的操作，有了这样的基础就进入到红黑树的讲解，因为它们都是依靠旋转来调衡树高的。但红黑树的五条限定规则来的那么突然，没有原因，没有道理。

这时候大部分资料会用2-3树来讲解红黑树，不过又不去实现一个2-3树，只是用了一个理论套另外一个理论。虽然能从理解上多一些参考，但始终感觉没有抓手呀。对于理科思维来说，你得给我东西呀。老是整这悬得楞的🥶谁能受了。所以这里我们先来用Java实现一个2-3树，有了基础再学习红黑树

# 二、2-3树数据结构

2–3树是一种树型数据结构，由约翰·霍普克洛夫特于1970年发明。它通过在一个节点存放1-2个元素来平衡树高。从而也使2-3树存在2叉节点和3叉节点。

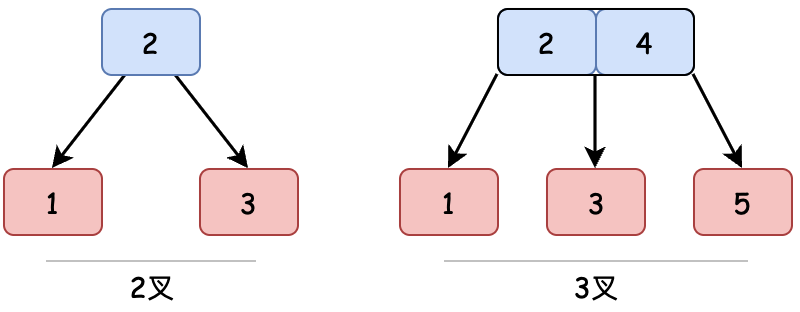
这里要提到一点，在BST二叉搜索树可能退化成链表的基础上。引出了自平衡二叉树，也就是包括上一章实现的AVL树和Java API HashMap中用到的红黑树，它们都属于BalancedTree，也统称为B树，平衡的意思。

而本章实现的2-3树也是一种简单的平衡树，其中每个具有子节点（内部节点）的节点要么有两个子节点（2 节点）和一个数据元素，要么有三个子节点（3 节点）和两个数据元素。另外 2-3 树是3阶B 树，2-3-4 树是4阶B树。

在实现2-3树之前，先通过图稿演示下在2-3树中顺序插入1、2、3、4、5、6、7，七个元素时，2-3树的调衡处理。

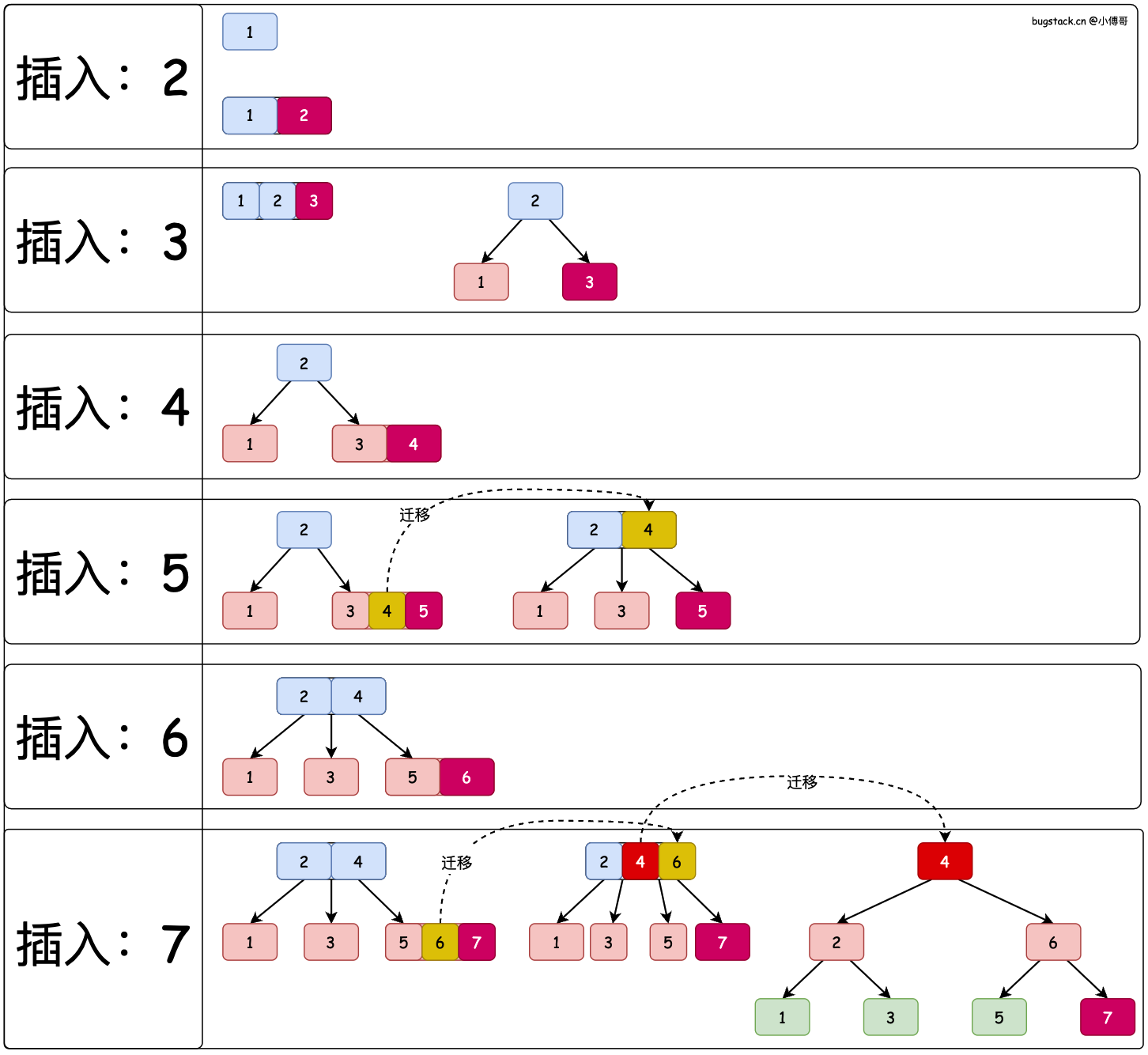
  • 2-3 树的插入过程与 BST 树类似，会通过树的左右节点大小，找到自己的插入位置。
  • 一个节点可以右1-3个元素，但当元素个数为3时，则需要调衡。把三个节点的中间节点晋升上来，其余两个节点为子节点。
  • 如果进行一次调衡后，上一层父节点达到3个元素，则需要2次调衡，来满足2-3树的规则。

咋样，是不看过这个图之后对于2-3树的实现已经有感觉了，想动手写写试试了？

# 三、2-3树结构实现

2-3 树的实现并不复杂，但在实现前要思考🤔以下几个问题；

  • Node 节点属性信息都包括什么？
  • 插入值，是否需要创建新的 Node？
  • 插入后，节点内有3个元素后，怎么迁移元素？

# 1. 节点定义

public class Node_2_3 {

    // 元素
    public int[] items;
    // 序号
    public int number;
    // 孩子
    public Node_2_3[] children;
    // 父亲【非必须】
    public Node_2_3 parent;

    public Node_2_3() {
        this.items = new int[3];
        this.number = 0;
        this.children = new Node_2_3[4];
        this.parent = null;
    }
    
    public void insert(int e) {
        int idx = this.number - 1;
        while (idx >= 0) {
            if (this.items[idx] < e) break;
            this.items[idx + 1] = this.items[idx];
            --idx;
        }
        this.items[idx + 1] = e;
        ++this.number;
    }
    
    // ... 省略部分代码
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
  • 2-3树的几点元素需要包括；一个数组的元素集合、元素的序号、孩子元素。因为一个节点最多可临时放入3个元素，那么就会最多有4个孩子元素，所以孩子元素也是一个数组并且在构造函数中按照4个元素进行初始化。
  • 由于本身2-3树插入元素的开始阶段，并不是直接创建一个新的节点，而是在初始化的数组空间中存入元素。所以在节点中提供了一个插入元素的方法 insert 来处理新增元素。
  • 另外2-3树的节点类，还提供了一个方便查询的方法。包括：获取左边元素、中间元素、右边元素，以及最小值、最大值和判断是否有孩子节点。这些内容可以源码。

# 2. 拆分节点

当一个节点内有3个元素的时候，就要发起拆分东西，拆分的过程分为；

  1. 对3个节点的中间节点，插入到父节点上。
  2. 剩余2个节点创建出新的节点。
  3. 建立父节点和新创建的2个节点间关系。

整个操作流程如图所示

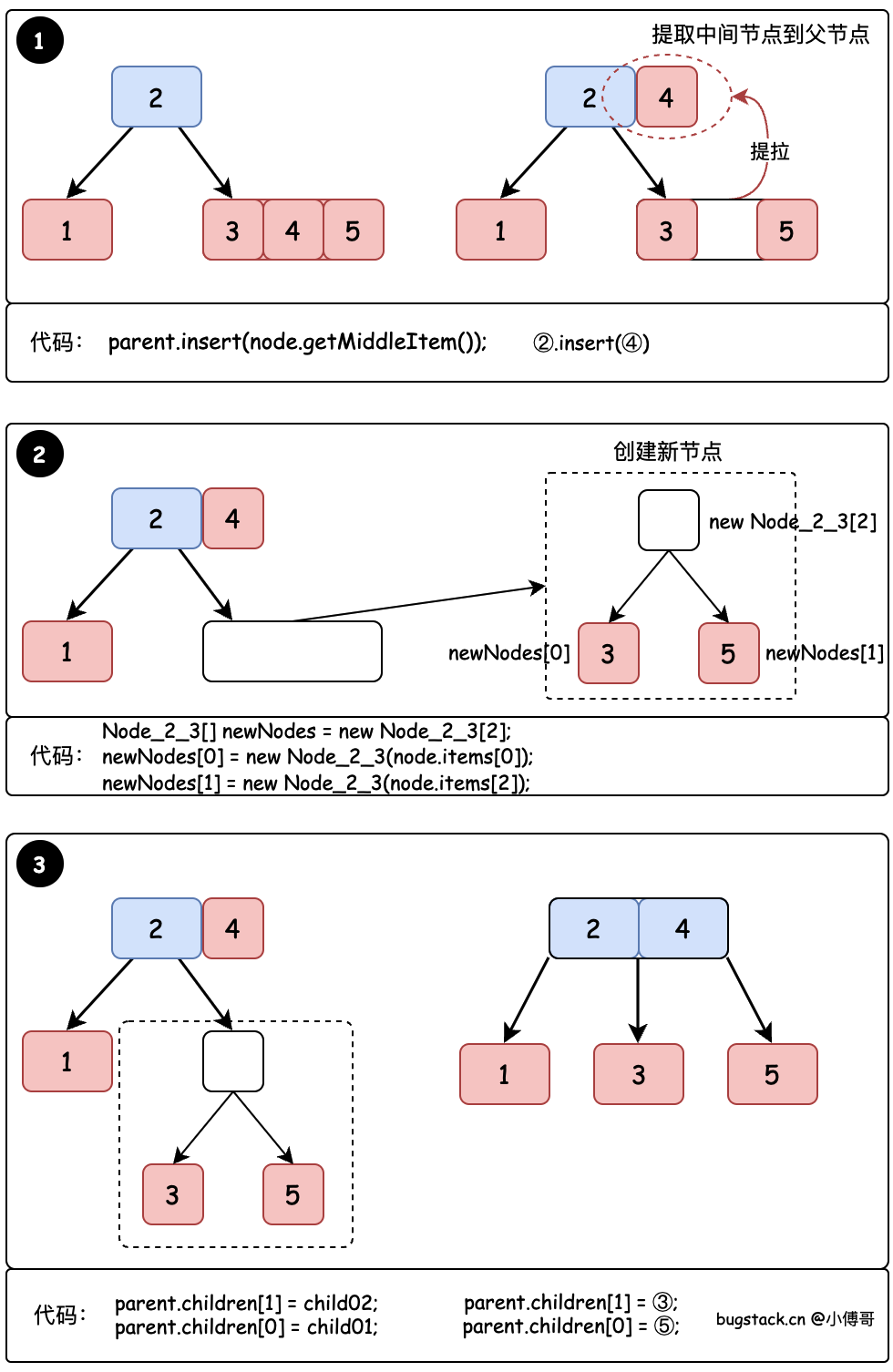
# 1. 插入父节点

private Node_2_3 split(Node_2_3 node, Node_2_3 parent) {
    if (parent == null) {
        parent = new Node_2_3(node);
    }
    
    parent.insert(node.getMiddleItem());
    
    Node_2_3[] newNodes = this.triangle(node);
    this.replaceChild(parent, node, newNodes[0], newNodes[1]);
    return parent;
}
1
2
3
4
5
6
7
8
9
10
11
  • 整个2-3树拆分的过程就是在 split 这个方法里，第一步解决了是否有父节点，没有则创建。
  • 之后将原节点的中间值插入到父节点中。接下来的操作就是拆分新节点和更换孩子节点建立新连接。

# 2. 拆分新节点

private Node_2_3[] triangle(Node_2_3 node) {
    Node_2_3[] newNodes = new Node_2_3[2];
    newNodes[0] = new Node_2_3(node.items[0]);
    newNodes[1] = new Node_2_3(node.items[2]);
    if (!node.isLeaf()) {
        // 左孩子
        newNodes[0].children[0] = node.children[0];
        newNodes[0].children[1] = node.children[1];
        // 右孩子
        newNodes[1].children[0] = node.children[2];
        newNodes[1].children[1] = node.children[3];
    }
    return newNodes;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
  • 基于传递进来的节点，将节点的左右孩子创建新节点，如果这个孩子节点还有分支节点，则一并更新。

# 3. 建立新连接

private void replaceChild(Node_2_3 parent, Node_2_3 oldChild, Node_2_3 child01, Node_2_3 child02) {
    if (oldChild == parent.children[0]) {
        parent.children[3] = parent.children[2];
        parent.children[2] = parent.children[1];
        parent.children[1] = child02;
        parent.children[0] = child01;
    } else if (oldChild == parent.children[1]) {
        parent.children[3] = parent.children[2];
        parent.children[2] = child02;
        parent.children[1] = child01;
    } else {
        parent.children[3] = child02;
        parent.children[2] = child01;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
  • 建立新连接需要判断这个节点 oldChild 是父节点的左、中、右，之后进行依次的更换。
  • 如拆分节点的介绍图中，用到的就是 parent.children[1] = child02;parent.children[0] = child01; 两步操作过程。

# 3. 新增节点

public void insert(int e) {
    // 记录元素
    elementList.add(e);
    // 插入元素
    if (root == null) {
        root = new Node_2_3(e);
    } else {
        root = insert(e, root);
        if (root.number == 3) {
            root = split(root, null);
        }
    }
}

private Node_2_3 insert(int e, Node_2_3 parent) {
    if (parent.isLeaf()) {
        parent.insert(e);
        return parent;
    }
    
    Node_2_3 child = null;
    if (parent.number == 1) {
        if (e < parent.getMinItem()) {
            child = insert(e, parent.getLeft());
        } else {
            child = insert(e, parent.getMiddle());
        }
    } else {
        if (e < parent.getMinItem()) {
            child = insert(e, parent.getLeft());
        } else if (e > parent.getMiddleItem()) {
            child = insert(e, parent.getRight());
        } else {
            child = insert(e, parent.getMiddle());
        }
    }
    
    if (child.number == 3) {
        return this.split(child, parent);
    }
    
    return parent;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
  • 新增节点的过程就比较简单了，一种是使用递归找到可以插入的位置，另外一种就是 where 循环。我们再BST、AVL两种数据结构种都是用了 where 循环。
  • 在2-3树中 insert 方法递归到对应的插入位置后，开始插入元素。当插入元素结束后判断这个节点是否已经达到了3个节点，如果是则进行拆分。拆分就调用了上面的步骤

# 四、2-3树结构测试

为了让读者更好的理解2-3树的结构，小傅哥在程序的控制台打印了插入的过程。网上没有2-3树在线的动画演示，如果读者看到也可以留言给小傅哥

@Test
public void test_insert_incr() {
    Tree_2_3 tree = new Tree_2_3();
    for (int i = 1; i <= 10; i++) {
        tree.insert(i);
        System.out.println(tree);
    }
}
1
2
3
4
5
6
7
8
  • 顺序插入10个节点，如果这是一颗BST树，它将会退化成链表。那么我们使用自平衡的2-3树，来看看它的插入效果。

测试效果

输入节点(1个)：1
 
[1]

输入节点(2个)：1,2
 
[1,2]

输入节点(3个)：1,2,3
 
 /----- [3]
[2]
 \----- [1]

输入节点(4个)：1,2,3,4
 
 /----- [3,4]
[2]
 \----- [1]

输入节点(5个)：1,2,3,4,5
 
 /----- [5]
[2,4]---- [3]
 \----- [1]

输入节点(6个)：1,2,3,4,5,6
 
 /----- [5,6]
[2,4]---- [3]
 \----- [1]

输入节点(7个)：1,2,3,4,5,6,7
 
         /----- [7]
 /----- [6]
 |       \----- [5]
[4]
 |       /----- [3]
 \----- [2]
         \----- [1]

输入节点(8个)：1,2,3,4,5,6,7,8
 
         /----- [7,8]
 /----- [6]
 |       \----- [5]
[4]
 |       /----- [3]
 \----- [2]
         \----- [1]

输入节点(9个)：1,2,3,4,5,6,7,8,9
 
         /----- [9]
 /----- [6,8]---- [7]
 |       \----- [5]
[4]
 |       /----- [3]
 \----- [2]
         \----- [1]

输入节点(10个)：1,2,3,4,5,6,7,8,9,10
 
         /----- [9,10]
 /----- [6,8]---- [7]
 |       \----- [5]
[4]
 |       /----- [3]
 \----- [2]
         \----- [1]


Process finished with exit code 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
  • 有了这样的数据结构示意，是不是再来看2-3树就非常清晰了。—— 我说过，理科生 + 技术，不要只抛理论，要看效果的！东西到手了，能拿捏了，再补充理论。

# 五、常见面试问题

  • 2-3树的数据结构描述
  • 2-3树一个节点最多可以存放几个元素
  • 2-3树插入节点时间复杂度
  • 2-3树一个节点有3个元素，如何迁移。需要旋转吗
  • 2-3树，你能手写一下吗？

← 红黑树 Red Back Tree →