小傅哥 bugstack 虫洞栈

# 数据结构：图 Graph

作者：小傅哥
博客：https://bugstack.cn (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

图的历史

Leonhard Euler 于1736 年发表的关于柯尼斯堡七桥 (opens new window)的论文被认为是图论史上的第一篇论文。这篇论文，以及范德蒙德写的关于骑士问题的论文，都是在莱布尼茨发起的分析位置上进行的。欧拉公式涉及凸多面体的边数、顶点数和面数，由 Cauchy 和L'Huilier 研究和推广，它代表了称为拓扑的数学分支的开始。

1860 年和 1930 年拓扑学的自主发展通过 Jordan、Kuratowski 和 Whitney 的著作使图论得以发展。图论和拓扑学 (opens new window)共同发展的另一个重要因素来自现代代数技术的使用。这种用途的第一个例子来自物理学家古斯塔夫·基尔霍夫的工作，他在 1845 年发表了他的基尔霍夫电路定律，用于计算电路中的电压和电流。

# 二、图的数据结构

图（Graph）结构是一种比树结构复杂的非线性的数据结构，图在实际生活中的例子非常多，比如；地铁线路网、微信好友关系链、计算机中的状态执行等，都可以抽象成图的结构。

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E) = 【G表示图、V表示顶点个数、E表示边的个数】。图的数据结构是多对多关系，就像你的微信好友可能也是我的微信好友，且相互交叉对应。与之对应的是树，树是1对多关系，所以树也是一种特殊的没有闭环的图。

按照图是否有方向和是否有权重可以分为一下4类组合；

U/U U/W D/U D/W
无向图&无权重 无向图&有权重 有向图&无权重 有向图&有权重
  • 顶点：图中的任意节点都算作顶点，图中任意两个顶点间都可能存在连接，如果没有顶点间没有连线则称为空图。
  • 无向图：图中任意两个顶点间都没有指向，则称这样的图为无向图。
  • 有向图：图中任意两个顶点间都有指向边，则称这样的图为有向图。
  • 无权重：图中任意两个顶点间的连线，没有权重值，则无权重。
  • 有权重：图中任意两个顶点间的连线，包含权重值，则有权重。

# 三、图的结构实现

图的结构实现可以基于数组、链表和红黑树实现，也因此将使用数组实现的图称为邻接矩阵，链表和红黑树实现的图称为邻接表。

// 图的顶点数
protected int v;
// 图的边个数
protected int e;

// 图的矩阵【数组】
protected int[][] table;
// 图的矩阵【链表】
protected LinkedList<Integer[]>[] table;
// 图的矩阵【红黑树】
private TreeSet<Integer>[] table;
1
2
3
4
5
6
7
8
9
10
11

图的数据存放可以使用 int 数组、LinkedList 链表、TreeSet 红黑树等方式存储。

# 1. 邻接矩阵【数组】

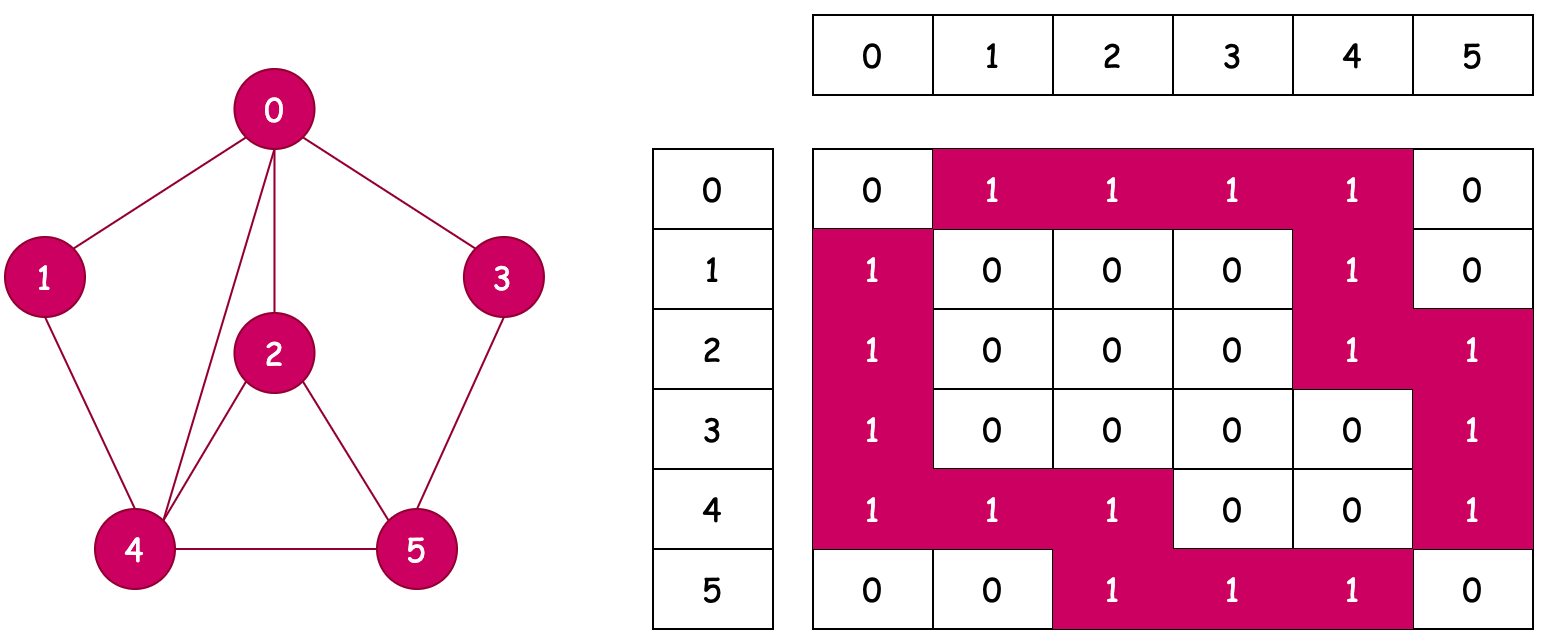
# 1.1 无向图&无权重

// 图的顶点数
protected int v;
// 图的边个数
protected int e;
// 图的矩阵
protected int[][] table;

// 对称插入，无方向，无权重
public void insert(int x, int y) {
    table[x][y] = 1;
    table[y][x] = 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
  • 邻接矩阵通过数组存放元素，会有一些浪费空间，所有的空间都会填满。
  • 在插入元素的时候，对称插入节点。例如：0→1、1→0，两个方向都插入元素。

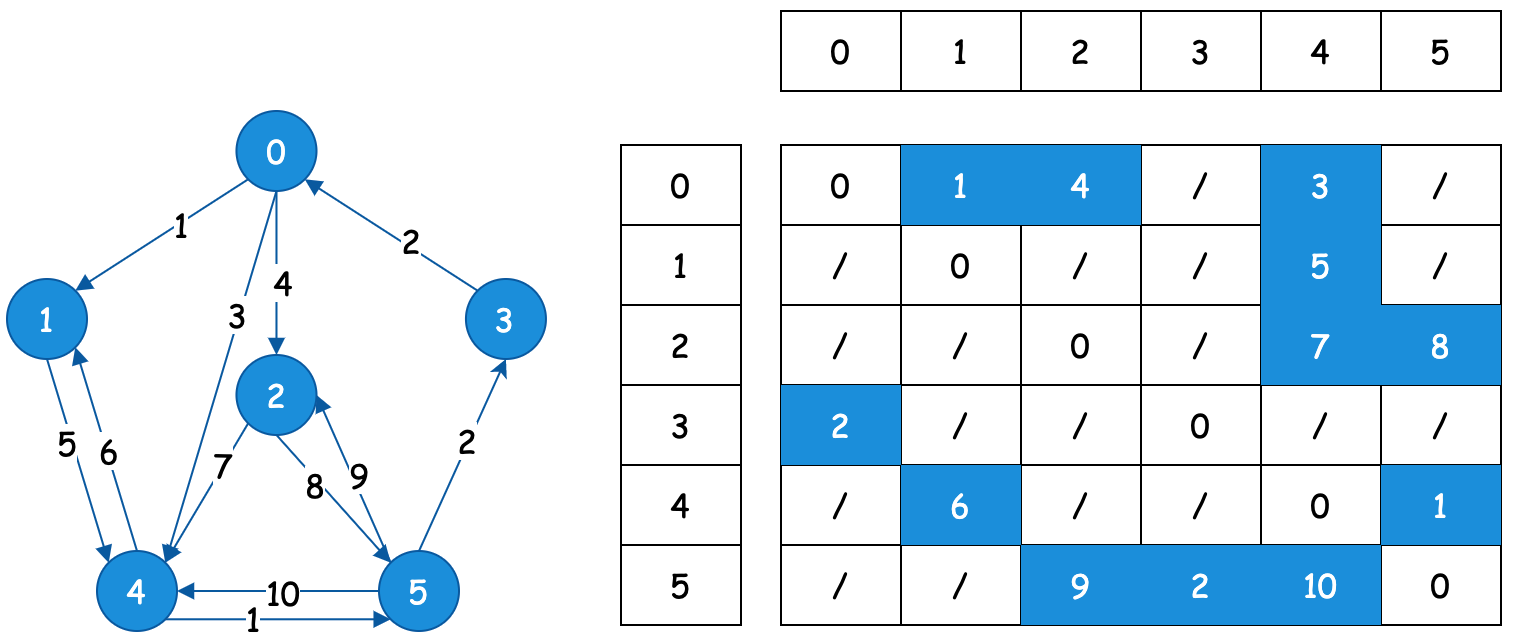
# 1.2 有向图&有权重

// 图的顶点数
protected int v;
// 图的边个数
protected int e;
// 图的矩阵
protected int[][] table;

// 对称插入，无方向，无权重
public void insert(int x, int y, int weight) {
    table[x][y] = weight;
}
1
2
3
4
5
6
7
8
9
10
11
  • 邻接矩阵通过数组存放元素，会有一些浪费空间，所有的空间都会填满。
  • 在插入元素的时候，插入单向节点，节点值为权重值。例如：0→2，权重值是4。

# 2. 邻接表【链表】

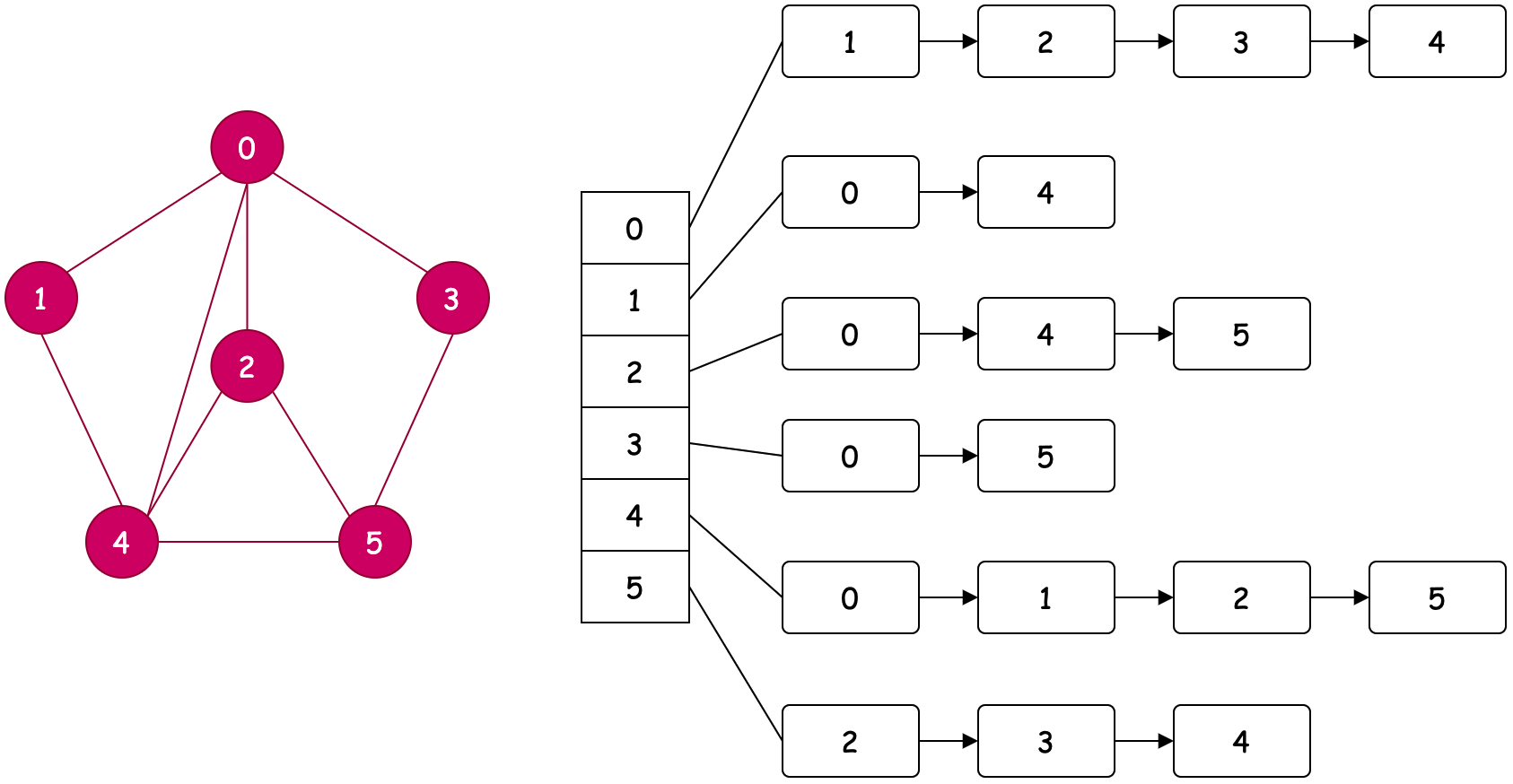
# 1.1 无向图&无权重

// 图的顶点数
protected int v;
// 图的边个数
protected int e;
// 图的矩阵
protected LinkedList<Integer[]>[] table;

// 对称插入，无方向，无权重
public void insert(int x, int y) {
    table[x].add(new Integer[]{y});
    table[y].add(new Integer[]{x});
}
1
2
3
4
5
6
7
8
9
10
11
12
  • 通过数组+链表的实现方式可以减少非必要的元素存储，更加节省空间。
  • 其实插入元素的过程和数组类似，无向无权重直接对称插入元素即可。

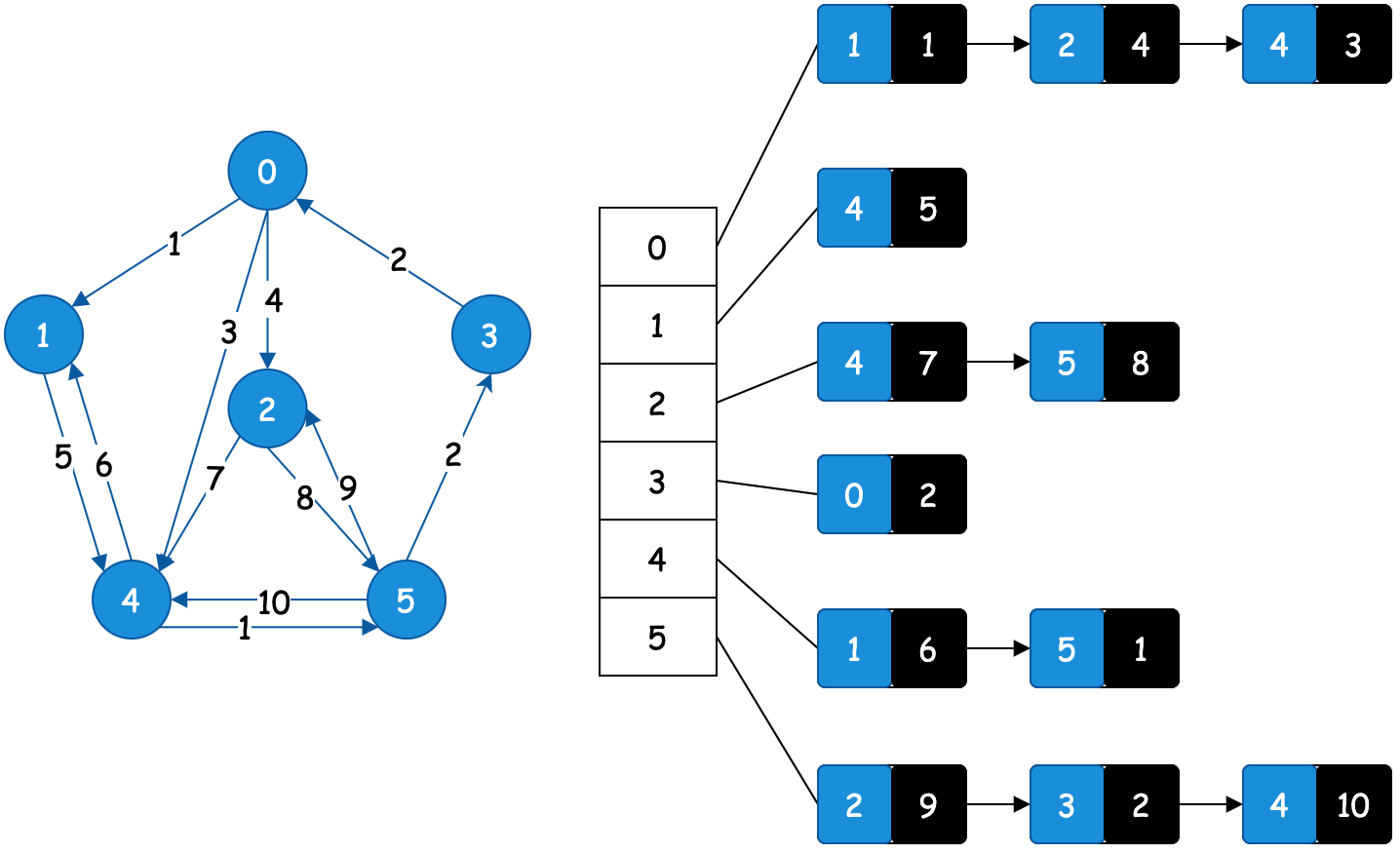
# 1.2 有向图&有权重

// 图的顶点数
protected int v;
// 图的边个数
protected int e;
// 图的矩阵
protected LinkedList<Integer[]>[] table;

// 对称插入，有方向，有权重
public void insert(int x, int y, int weight) {
    table[x].add(new Integer[]{y, weight});
}
1
2
3
4
5
6
7
8
9
10
11
  • 通过数组+链表的实现方式可以减少非必要的元素存储，更加节省空间。
  • 其实插入元素的过程和数组类似，有方向有权重则只插入单个指向，并需要通过数组或者对象的方式记录权重值。

# 3. 遍历

图的最终实现是通过 TreeSet 红黑树的方式，这样即节省空间，又能提高元素的索引和遍历效率。

// 图的顶点数
private int v;
// 图的边个数
private int e;
// 图的矩阵
private TreeSet<Integer>[] table;
1
2
3
4
5
6

# 3.1 无向图&有向图

无向图 有向图
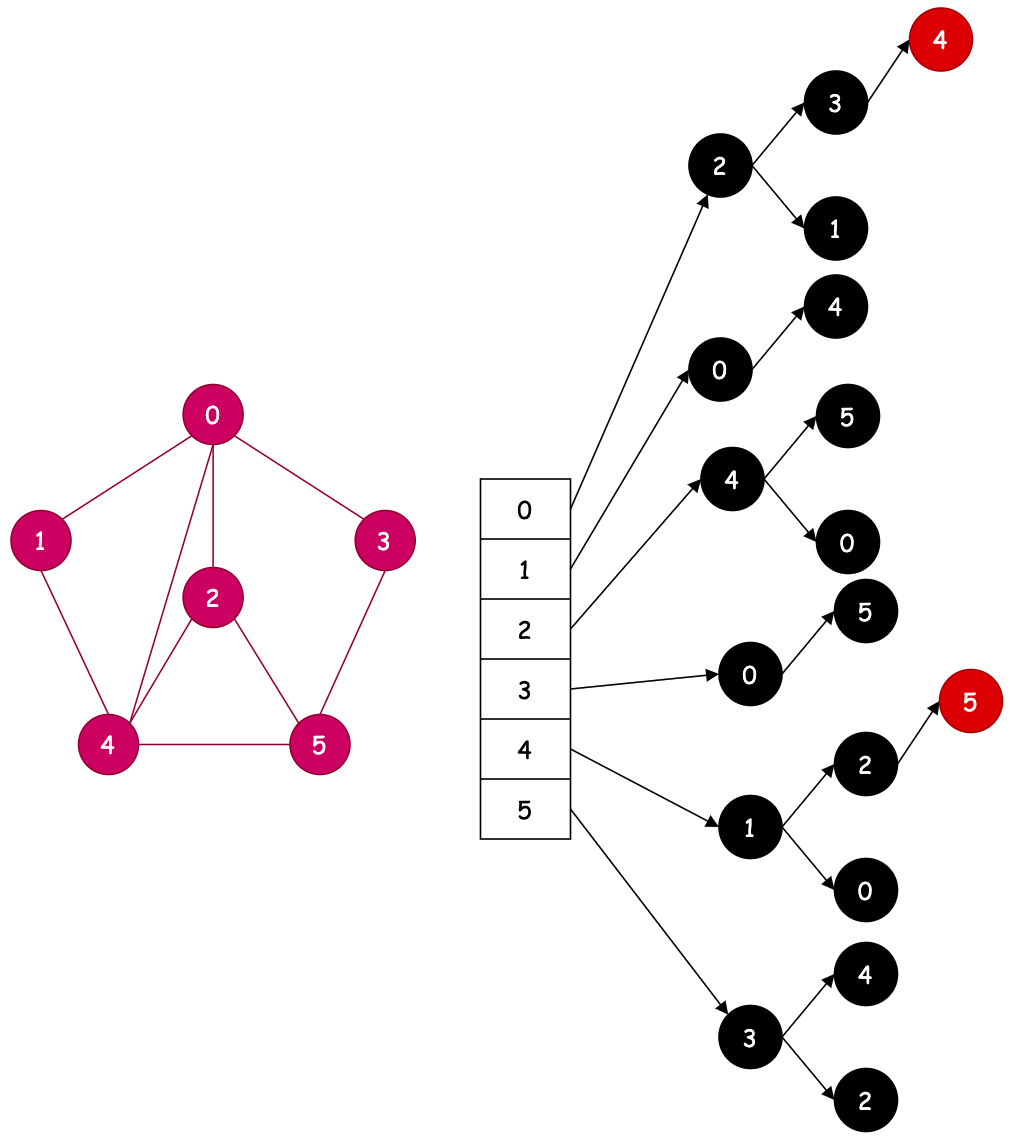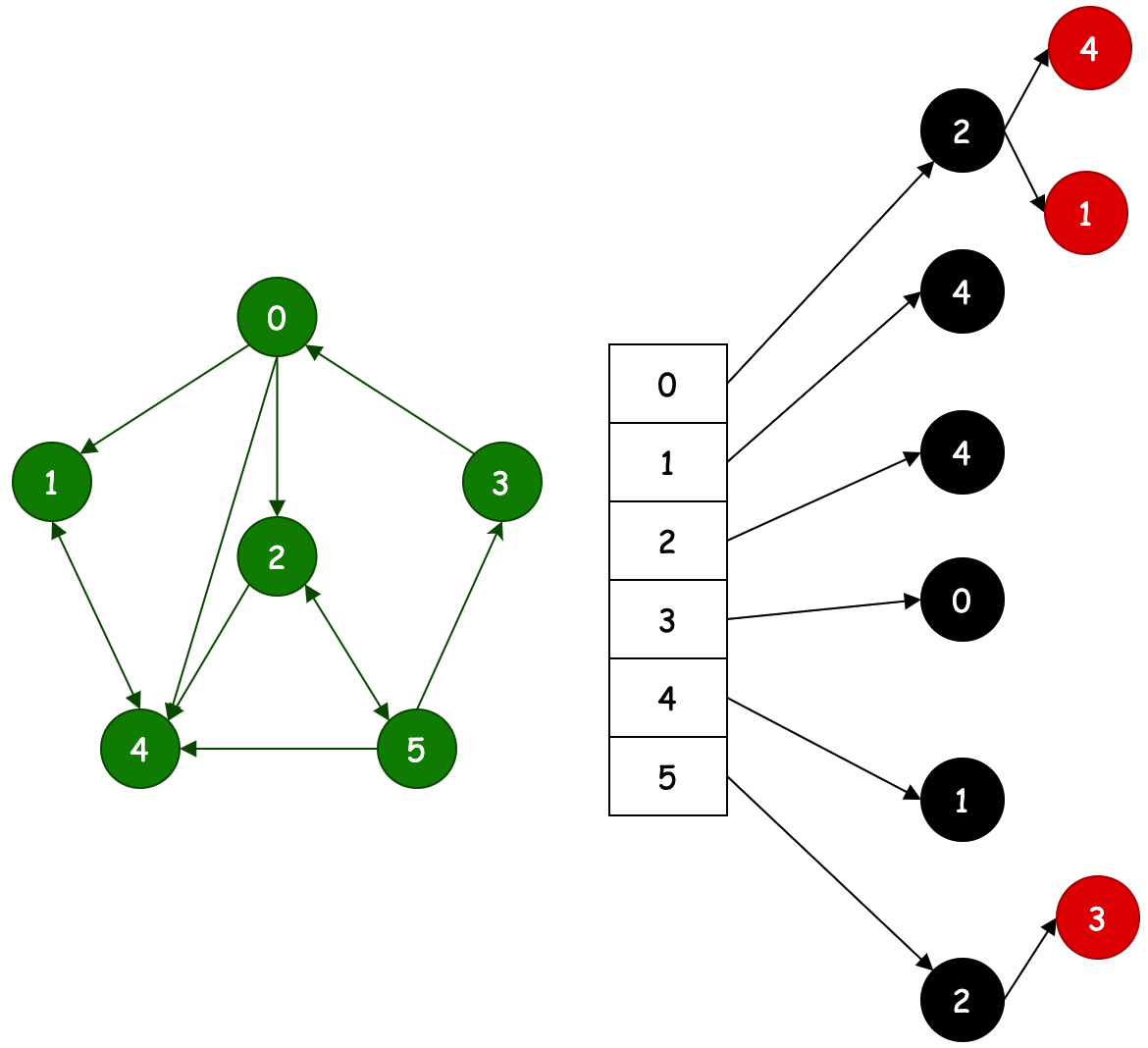对称插入：table[x].add(y); table[y].add(x); 单向插入：table[x].add(y);

# 3.2 广度遍历&深度遍历

U/U U/U D/U D/U
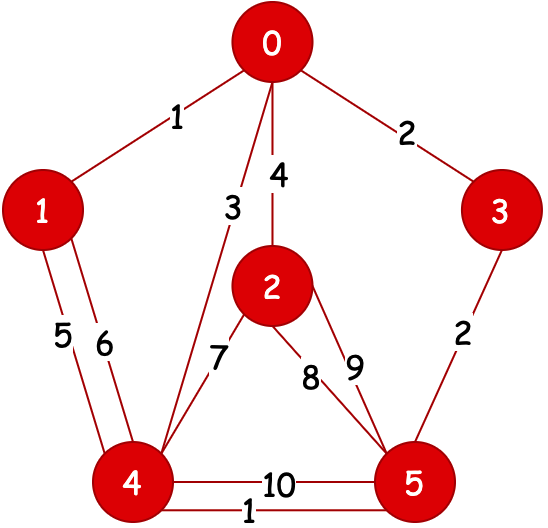
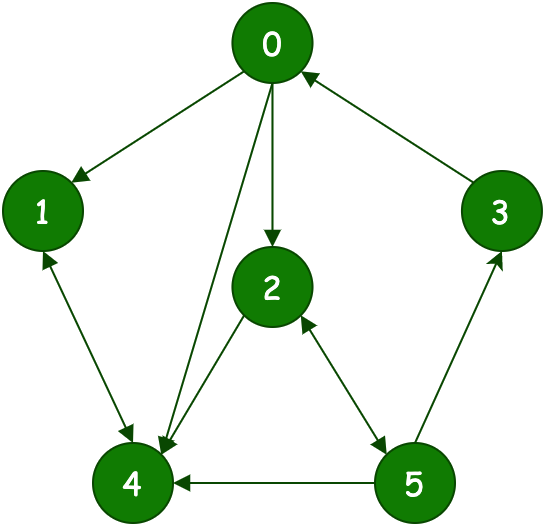
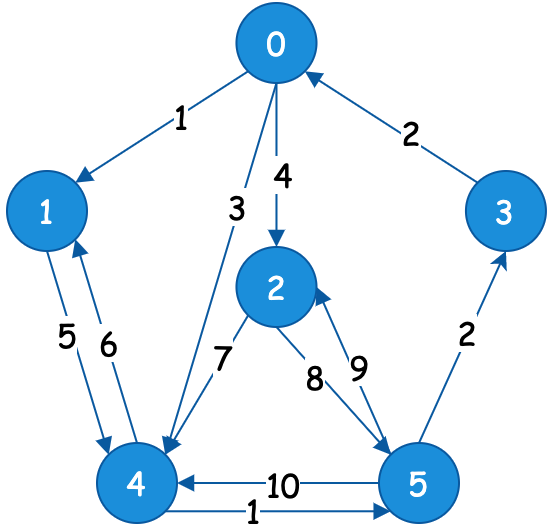
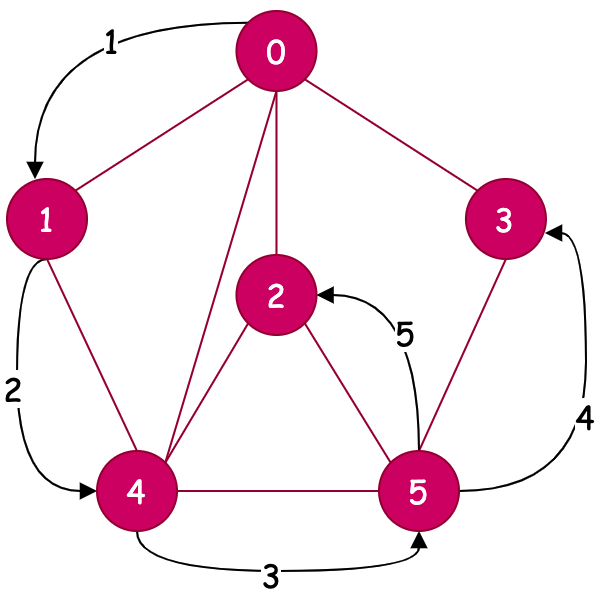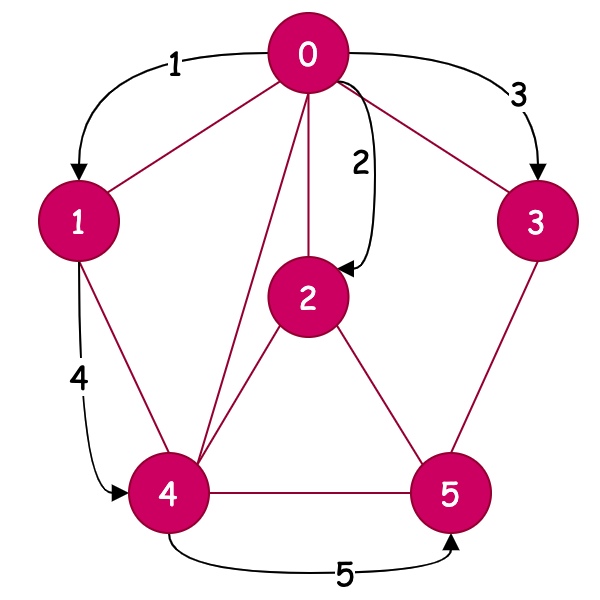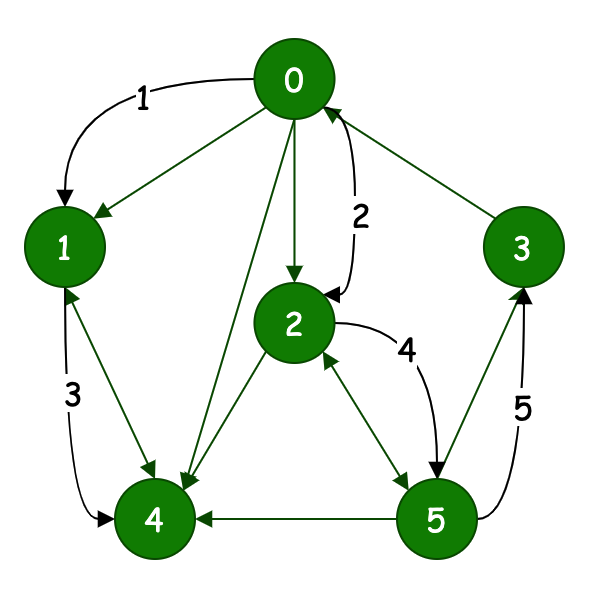深度遍历 广度遍历 深度遍历 广度遍历

通过四个图的的对比，可以看到；

  1. 深度遍历，不断地向下探测。广度遍历横行探测。
  2. 当有权重时候，则深度和广度会按照权重进行选择优先遍历的顺序。
public void bfs(int s) {
    Queue<Integer> queue = new LinkedList<>();
    visited[s] = true;
    queue.add(s);
    while (!queue.isEmpty()) {
        int v = queue.remove();
        order.add(v);
        for (int w : G.adj(v)) {
            if (!visited[w]) {
                queue.add(w);
                visited[w] = true;
            }
        }
    }
}

private void dfs(int v) {
    visited[v] = true;
    // 深度优先，前序遍历
    pre.add(v);
    for (int w : graph.adj(v)) {
        if (!visited[w]) {
            dfs(w);
        }
    }
    // 深度优先，后序遍历
    post.add(v);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 四、图实现测试

# 1. 邻接矩阵

@Test
public void test_U_U() {
    AdjacencyMatrixArray.U_U matrix = new AdjacencyMatrixArray.U_U(6, 9);
    matrix.insert(0, 1);
    matrix.insert(0, 3);
    matrix.insert(0, 2);
    matrix.insert(0, 4);
    matrix.insert(1, 4);
    matrix.insert(2, 4);
    matrix.insert(2, 5);
    matrix.insert(3, 5);
    System.out.println(matrix);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
  • 在单元测试中共提供了UU、UW、DU、DW四种情况，读者可自行验证。
图配置：V = 6, E = 9
---------------------------
  | 0 | 1 | 2 | 3 | 4 | 5 | 
⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛⏛
0 | 0 | 1 | 1 | 1 | 1 | 0 | 
---------------------------
1 | 1 | 0 | 0 | 0 | 1 | 0 | 
---------------------------
2 | 1 | 0 | 0 | 0 | 1 | 1 | 
---------------------------
3 | 1 | 0 | 0 | 0 | 0 | 1 | 
---------------------------
4 | 1 | 1 | 1 | 0 | 0 | 0 | 
---------------------------
5 | 0 | 0 | 1 | 1 | 0 | 0 | 
---------------------------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
  • 通过测试结果可以看到一个邻接矩阵无向图且无权重的存放结果。

# 2. 邻接链表

@Test
public void test_D_W() {
    AdjacencyMatrixList.D_W matrix = new AdjacencyMatrixList.D_W(6, 9);
    matrix.insert(0, 1, 1);
    matrix.insert(0, 3, 2);
    matrix.insert(0, 2, 3);
    matrix.insert(0, 4, 5);
    matrix.insert(1, 4, 1);
    matrix.insert(2, 4, 3);
    matrix.insert(2, 5, 7);
    matrix.insert(3, 5, 4);
    System.out.println(matrix);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
  • 在单元测试中共提供了UU、UW、DU、DW四种情况，读者可自行验证。

测试结果

图配置：V = 6, E = 9
---------------------------
0 | → [1,1] → [3,2] → [2,3] → [4,5]
---------------------------
1 | → [4,1]
---------------------------
2 | → [4,3] → [5,7]
---------------------------
3 | → [5,4]
---------------------------
4 |
---------------------------
5 |
---------------------------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
  • 通过测试结果可以看到邻接链表在对图元素的存储上，非常节省空间，并记录了权重值。

# 五、常见面试题

  • 图的使用场景是什么？
  • 图有的分类？
  • 图怎么存放权重值？
  • 图的广度遍历
  • 图的深度遍历

← 布隆过滤器 Bloom Filter →