# 野路子搞算法 · 让算法可视化《leetcode03.无重复字符的最长子串》
小傅哥 & https://bugstack.cn (opens new window)
沉淀、分享、成长,专注于原创专题案例,以最易学习编程的方式分享知识,让自己和他人都能有所收获。目前已完成的专题有;Netty4.x实战专题案例、用Java实现JVM、基于JavaAgent的全链路监控、手写RPC框架、架构设计专题案例、源码分析、算法学习等。
你用剑🗡、我用刀🔪,好的代码都很烧,望你不吝出招!
# 一、前言
在刷了第一道 leetcode 的题以后我一直在思考,怎么才能让小白更清楚的了解到整个算法运行的过程。如果只是单纯的一点点看代码,从中摸清楚整个流程确实还是有一些难度。虽然就一道题来说,代码块并不会很大,但仅凭借变量之间的交换以及断点调试输出结果,还是很难在我们的大脑中形成一个完整的执行流程。
为此,最近经过不断的搜索在 Github 中找到了 MarkKoz (opens new window) 大神的算法可视化工程:algorithm-visualizer (opens new window) 。这是 nodejs 代码,在按照文档说明安装以及写测试用例验证后,确实可以满足目前的可视化需求。
好!那么我就按照自己的需求,将代码部署到本地以及创建了一套符合自己需求可以将各种算法题进行可视化展示。这套功能包括三部分,如下(可以下载后运行);
| 序号 | 名称 | 功能 | 操作 |
|---|---|---|---|
| 1 | algorithm-visualizer | 可视化算法代码平台,目前支持的算法包括回溯法、加密算法、动态规划、图搜索、贪婪算法、搜索算法、排序算法等。 | 下载 (opens new window) |
| 2 | server | 算法可视化服务器,用于编译算法代码提供服务接口。这个编译过程会从 github 上下载算法代码,并编译到本地。 | 下载 (opens new window) |
| 3 | algorithms | 算法代码块,这里面默认包括了大量的可执行展示的算法。同时在我们刷 leetcode 后也是将代码编写为可视化的方式,提交到这里。 | 下载 (opens new window) |
效果展示:
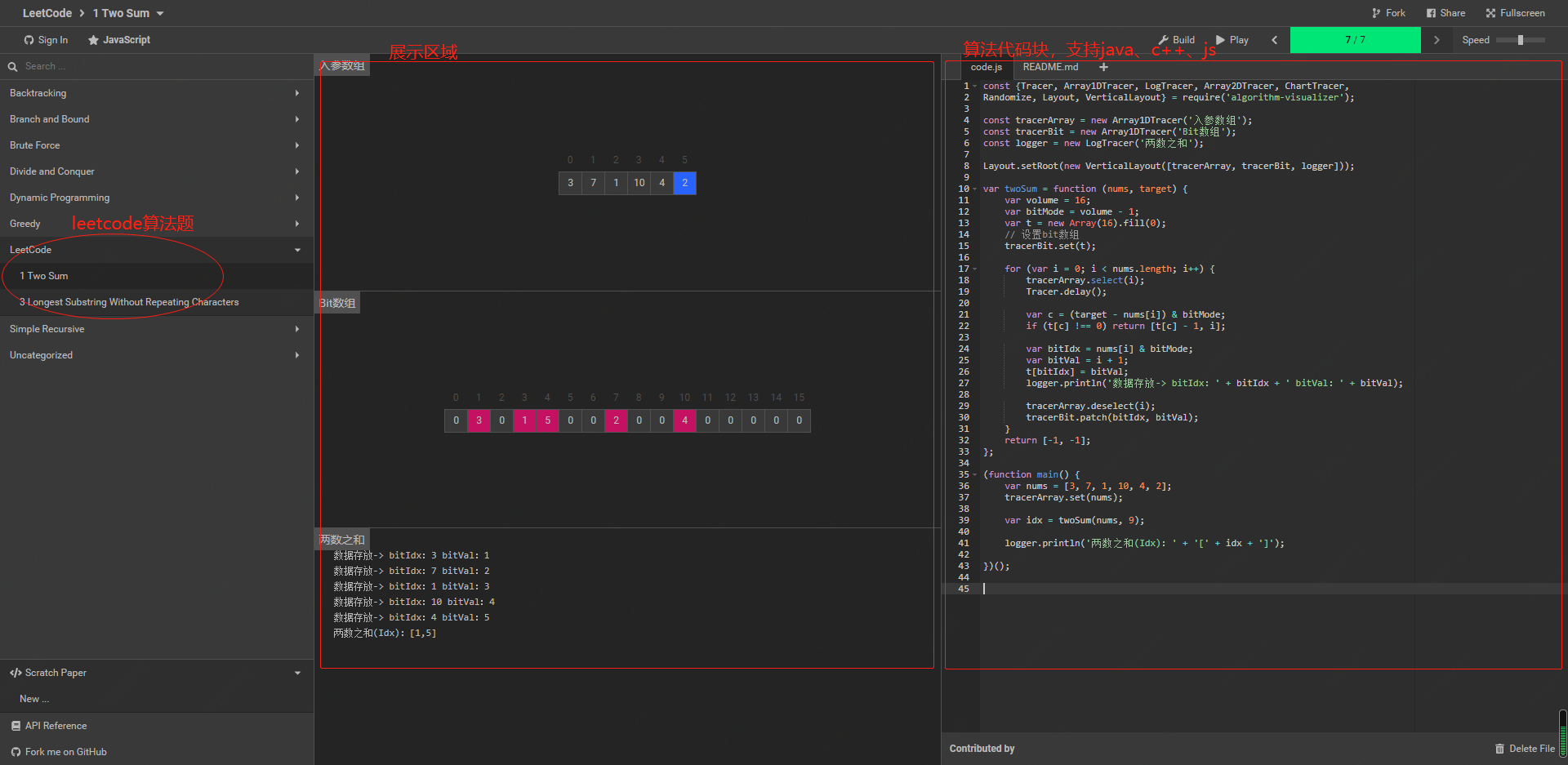
- 最左侧是代码区域,也就是我们提交到
algorithms中的算法代码。不支持中文以及特殊符号 - 中间是展示运行过程区域,这部分主要来自于在算法代码中添加的展示化代码块,例如:
array1DTracer.select(beginIdx, i - 1); - 最右侧是代码区域,这里的代码可以修改后构建并运行,但不会保存。同时在运行的时候可以调整运行速度
Speed,极大的方便了我们观察算法的执行过程 - 上图的展示内容其实就是我们在
leetcode中做的第一题《两数之和》其中的一中使用自己定义的bit结构数组的方式求解的演示
那么!接下来我们开始刷 leetcode 中第三题《无重复字符的最长子串》,并最终动态展示给大家这段算法的执行效果。如果你想在本地运行,可以关注公众号:bugstack虫洞栈
# 二、题目:《无重复字符的最长子串》
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
2
3
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
2
3
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
2
3
4
java
class Solution {
public int lengthOfLongestSubstring(String s) {
// TODO
}
}
2
3
4
5
# 三、思路和实现
从题目和示例上可以分析到这个题主要是从字符串中顺序寻找出一串内部不重复又是整个字符串中最长的那个字串。为了寻找到这样的子串可能首先想到的是循环出所有子串的集合,之后选取最长的。当把整个思路在整理几遍和简化后,那么是不就可以理解为,这是两个值指针在字符串中往前跑,当结尾指针碰到的元素与开始指针指向的元素一致,则将开始指针向前进一位,之后继续执行直到结束算出最长子串。整个思路可以用下图展示;
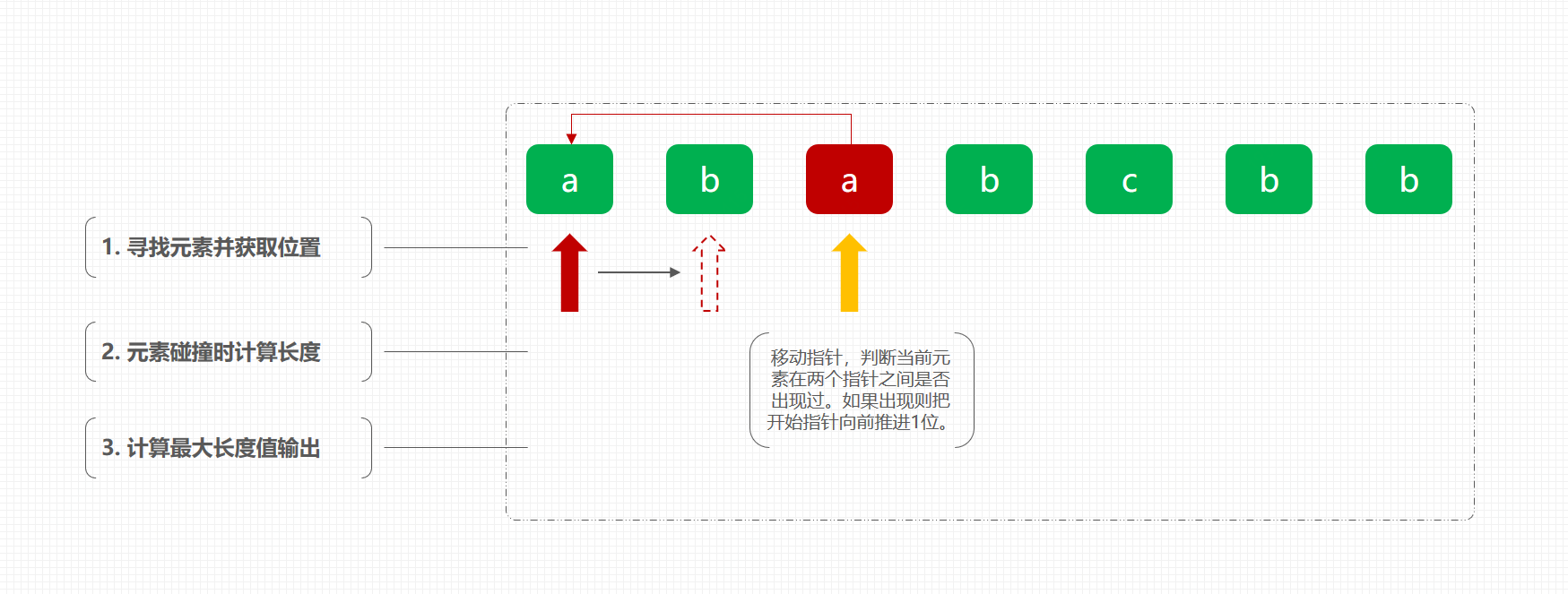
- 从上图的算法可以看到,只要先跑的那个指针也就是子串结尾的指针,碰到了开始指针中间,一样的元素,就将指针位置指向相同元素的下一位。切记不是指针 +1
- 为了实现这样的功能,我们就需要存储两个指针,同时需要有方法判断元素所处的位置。那么有如下几个方法;
- 使用
indexOf,整个方法可以判断元素位置,同时可以指定从某个位置开始判断后面的元素是否存在相同元素。 - 使用
toCharArray(),转换为数组,并将元素按照按照编码位置存放到新建的数组中,用于判断元素是否出现过。 - 使用
bit,建立一个数组结构,通过与运算获取元素位置,并存放。方便快速查找。
- 使用
- 另外在比对是否撞上相同元素的时候,可以输出当前开始指针与结束指针中间的长度,并与之前的记录的值比对,如果超过则更新,直到最后输出。
# 1. 实现方式,indexOf
public int lengthOfLongestSubstring_1(String s) {
if (null == s || "".equals(s)) return 0;
if (" ".equals(s) || s.length() == 1) return 1;
int beginIdx = 0, endIdx = 0, maxSize = 0;
for (int i = 1; i < s.length(); i++) {
endIdx = i;
int existIdx = s.indexOf(s.charAt(i), beginIdx);
if (existIdx < endIdx) {
beginIdx = existIdx + 1;
}
int eval = endIdx - beginIdx + 1;
if (maxSize < eval) {
maxSize = eval;
}
}
return maxSize;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- 不满足条件的字符串直接按照规则返回。
- 每次循环计算是否碰撞到相同的元素,并处理开始指针的位置。
- 最后输出最长子串的长度。
# 2. 实现方式,toCharArry
public int lengthOfLongestSubstring_2(String s) {
if (null == s || "".equals(s)) return 0;
if (" ".equals(s) || s.length() == 1) return 1;
char[] array = s.toCharArray();
int[] exist = new int[127];
exist[array[0]] = 1;
int beginIdx = 1, endIdx = 1, maxSize = 0;
for (int i = 1; i < array.length; i++) {
endIdx = i;
if (exist[array[i]] >= beginIdx) {
maxSize = Math.max(i - beginIdx + 1, maxSize);
beginIdx = exist[array[i]] + 1;
}
exist[array[i]] = i + 1;
}
maxSize = Math.max(exist[array[endIdx]] - beginIdx + 1, maxSize);
return maxSize;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- 同样不满足的字符串直接返回。
- 字符串转换为数组,同时定义一个新的数组用于存放地址。
int[] exist = new int[127],元素作为地址,位置作为值。 - 只有在碰撞时候才计算两个指针间的长度,其他时间不计算。
- 最后输出最长子串的长度。
# 3. 实现方式,bit结构
public int lengthOfLongestSubstring_3(String s) {
if (null == s || "".equals(s)) return 0;
if (" ".equals(s) || s.length() == 1) return 1;
int volume = 128;
int bitMode = volume - 1;
int[] t = new int[volume];
int beginIdx = s.charAt(0) & bitMode, endIdx = 0, maxSize = 0;
t[beginIdx] = 1;
for (int i = 1; i < s.length(); i++) {
endIdx = s.charAt(i) & bitMode;
int val = t[endIdx];
if (val != 0 && val >= t[beginIdx]) {
beginIdx = s.charAt(val) & bitMode;
t[beginIdx] = val + 1;
}
t[endIdx] = i + 1;
int v = t[endIdx] - t[beginIdx] + 1;
if (v > maxSize) {
maxSize = v;
}
}
return maxSize;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 如果你把上面的代码看明白了,那么这块的逻辑变化只是在于将元素通过
与运算存放到bit结构中,这和我们在计算《两数之和》的算法方式一样。
# 四、算法可视化运行

- 通过可视化运行可以很方便的看到算法的执行过程,这要比我们只是用脑子一遍遍过程流程清晰的多。尤其是对新人来说,简直太方便了。
- 这个可视化运行的工具,可以自己下载安装,他是nodejs的环境。如果在使用过程中遇到什么问题,可以关注公众号(bugstack虫洞栈)内联系我。
# 五、总结
- 想做好算法目前看到最主要的是捋清楚它的执行思路,之后选择不同的数据结构进行填充数据。最后按照这个流程一点点调试算法,以满足所有情况。
- 在可视化工具的辅助下,可以更加轻松的看到算法内部的执行过程。并且将算法转换为可视化,也不是很复杂,只要按照标准编写即可。
- 如果你也是一个爱做算法题的小白或者大牛,也欢迎你加入我们的算法可视化中,让我们一起开始算法之旅:https://github.com/niubility-algorithm (opens new window)

