小傅哥 bugstack 虫洞栈

# 《程序员数学：阶乘》—— 阶乘的用途是什么？

作者：小傅哥
博客：https://bugstack.cn (opens new window)
源码：https://github.com/fuzhengwei/java-algorithms (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

阶乘的历史

早在12世纪，印度学者就已有使用阶乘的概念来计算排列数的纪录。1677年时，法比安·斯特德曼使用Change ringing来解释阶乘的概念。在描述递归方法之后，斯特德将阶乘描述为：“现在这些方法的本质是这样的：一个数字的变化数包含了所有比他小的数字（包括本身）的所有变化数……因为一个数字的完全变化数是将较小数字的变化数视为一个整体，并透过将所有数字的完整变化联合起来。”

# 二、定义

阶乘可通过连续乘积来定义：n!=1·2·3···(n-2)·(n-1)·n

用连乘积符号可表示为：

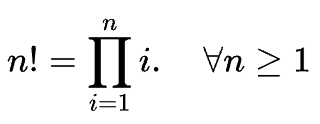
从上述公式中，可以推导出递推关系：n!=n·(n-1)!

但递归定义须给出base case，因此需要定义零的阶乘。 除此之外，递推关系在阶乘函数中各个值皆成立，例如：

  • 5!=5·4!
  • 6!=6·5!
  • 50!=50·49!

# 三、实现

递归实现

public class Factorial {

    public long factorial(long number) {
        if (number <= 1)
            return 1;
        else {
            return number * factorial(number - 1);
        }
    }

}
1
2
3
4
5
6
7
8
9
10
11
  • 就是一个简单的递归调用，实现起来还是蛮简单的。

# 四、测试

单元测试

@Test
public void test() {
    Factorial factorial = new Factorial();
    long result = factorial.factorial(5);
    System.out.println("测试结果：" + result);
}
1
2
3
4
5
6
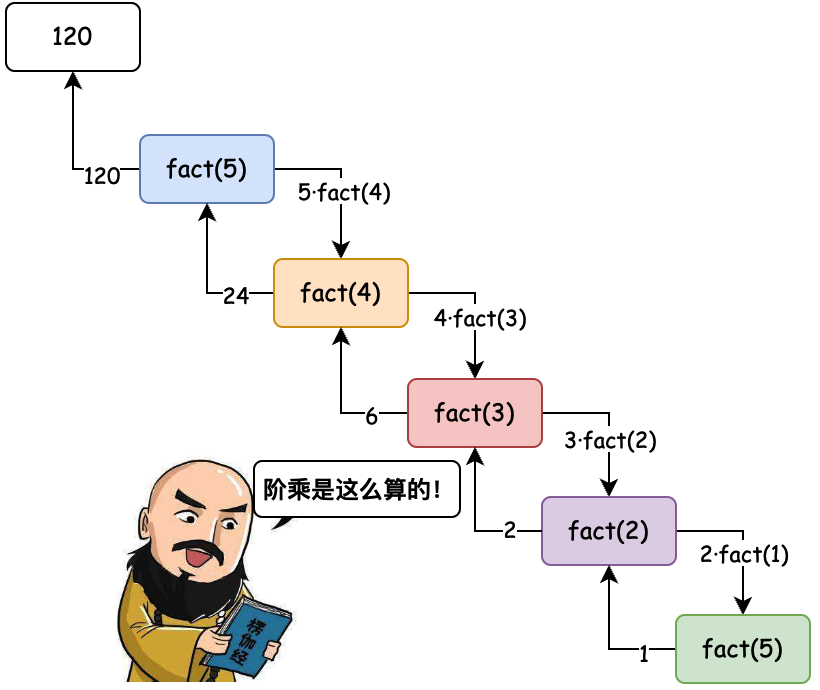
  • 计算5的阶乘，测试结果120

← 斐波那契 fibonacci →