小傅哥 bugstack 虫洞栈

# 《程序员数学：排列》- 有/无重复

作者：小傅哥
博客：https://bugstack.cn (opens new window)
源码：https://github.com/fuzhengwei/java-algorithms (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

这是一个高中阶段非常常见的数学问题，排序。有 ABC 三个字母，可重复使用字母和不可重复使用字母，都有多少种组合方式。对于这样的问题可以使用公式 A! C! 来计算，不知道你是否已经忘记。

不重复，组合数：n * (n-1) * (n -2) * ... * 1 = n!

可重复，组合数：n * n * n ... (r times) = n^r

这样的计算到不难，但作为程序员我们常常需要把这样的数学问题，用代码逻辑给体现出来。并且还需要考虑一个时间复杂度的问题。

# 二、实现

# 1. 无重复

public static List<List<Integer>> permutationWithRepetitions(int[] permutationOptions, int permutationLength) {
    if (permutationLength == 1) {
        List<List<Integer>> result = new ArrayList<>();
        for (int permutationOption : permutationOptions) {
            List<Integer> item = new ArrayList<>();
            item.add(permutationOption);
            result.add(item);
        }
        return result;
    }
    List<List<Integer>> permutations = new ArrayList<>();
    List<List<Integer>> smallerPermutations = permutationWithRepetitions(permutationOptions, permutationLength - 1);
    for (int currentOption : permutationOptions) {
        for (List<Integer> smallerPermutation : smallerPermutations) {
            List<Integer> permutation = new ArrayList<>();
            permutation.add(currentOption);
            permutation.addAll(smallerPermutation);
            permutations.add(permutation);
        }
    }
    return permutations;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

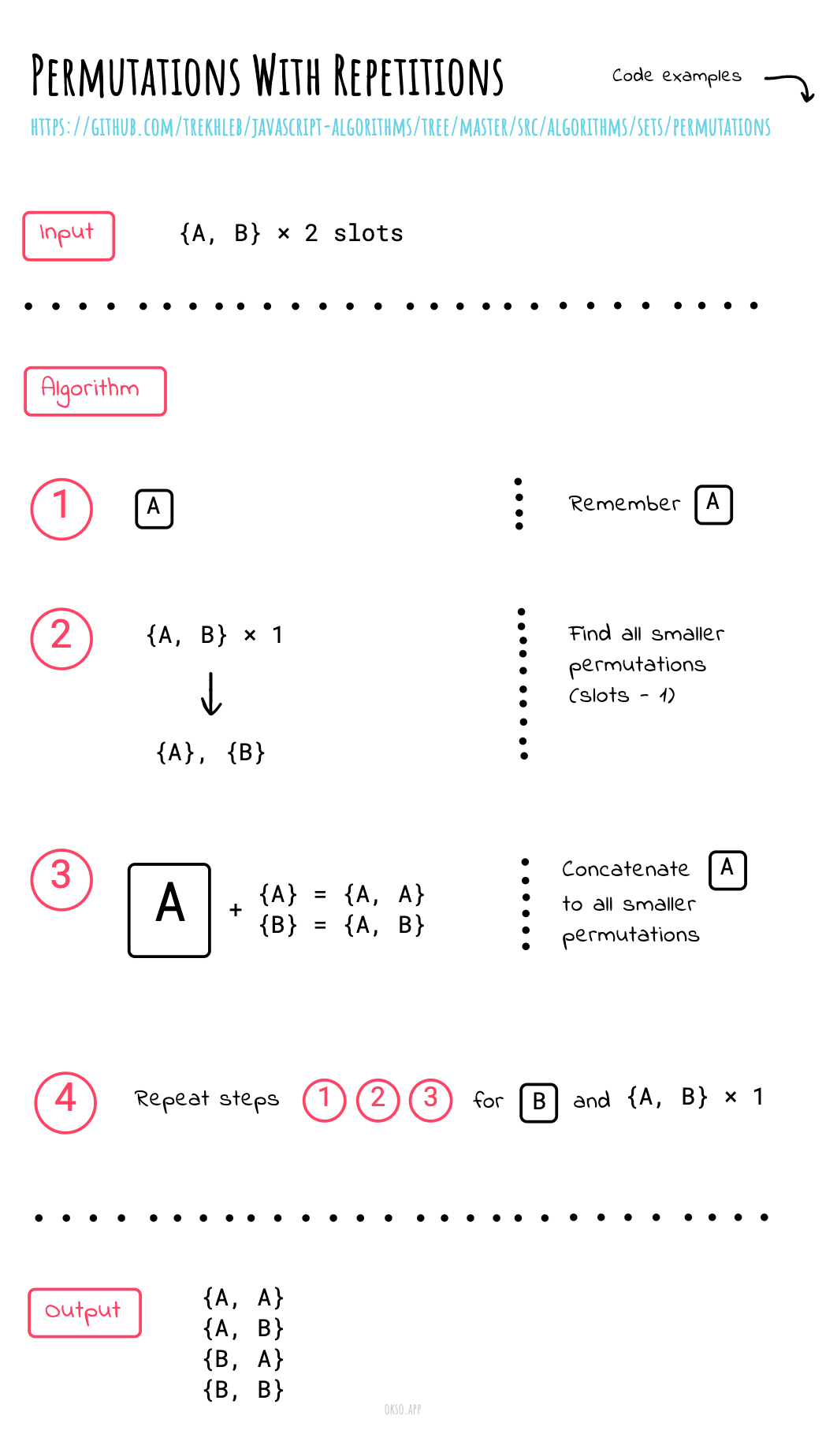
  • 这段代码是一个 Java 函数，它生成带重复元素的排列组合。它接受两个参数：

    • permutationOptions：排列元素的数组。
    • permutationLength：排列的长度，默认为 permutationOptions 的长度。

  • 算法使用递归的方式，如果排列的长度为 1，则将 permutationOptions 数组的每个元素作为一个列表返回；

  • 否则，首先获取不包括第一个元素的小排列，然后将第一个元素插入到每个小排列的每个可能位置上，生成所有排列组合。最后，返回排列组合的列表。

# 2. 可重复

public static List<List<Integer>> permutationWithoutRepetitions(int[] permutationOptions) {
    if (permutationOptions.length == 1) {
        List<List<Integer>> result = new ArrayList<>();
        result.add(List.of(permutationOptions[0]));
        return result;
    }
    List<List<Integer>> permutations = new ArrayList<>();
    int[] smallerOptions = new int[permutationOptions.length - 1];
    System.arraycopy(permutationOptions, 1, smallerOptions, 0, smallerOptions.length);
    List<List<Integer>> smallerPermutations = permutationWithoutRepetitions(smallerOptions);
    int firstOption = permutationOptions[0];
    for (List<Integer> smallerPermutation : smallerPermutations) {
        for (int positionIndex = 0; positionIndex <= smallerPermutation.size(); positionIndex++) {
            List<Integer> permutationPrefix = new ArrayList<>(smallerPermutation.subList(0, positionIndex));
            List<Integer> permutationSuffix = new ArrayList<>(smallerPermutation.subList(positionIndex, smallerPermutation.size()));
            List<Integer> permutation = new ArrayList<>(permutationPrefix);
            permutation.add(firstOption);
            permutation.addAll(permutationSuffix);
            permutations.add(permutation);
        }
    }
    return permutations;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
  • 这段 Java 代码实现了一个递归算法，它生成不带重复项的整数序列的全排列。它首先特判了如果传入的数组只有一个元素，那么返回一个只包含这个元素的 List。
  • 否则它将传入的数组分为两部分：第一个元素和剩下的元素。它先递归计算剩下的元素的全排列，然后将第一个元素插入到每个全排列的每一个可能位置。最后将所有的排列组合起来，返回结果。

# 三、测试

@Test
public void test_permutationWithRepetitions() {
    int[] permutationOptions = {1, 2, 3};
    List<List<Integer>> permutation = Permutations.permutationWithRepetitions(permutationOptions, 2);
    for (List<Integer> list : permutation) {
        System.out.println(JSON.toJSONString(list));
    }
}

@Test
public void test_permutationWithoutRepetitions() {
    int[] permutationOptions = {1, 2, 3};
    List<List<Integer>> permutation = Permutations.permutationWithoutRepetitions(permutationOptions);
    for (List<Integer> list : permutation) {
        System.out.println(JSON.toJSONString(list));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

测试结果

[1,1]
[1,2]
[1,3]
[2,1]
[2,2]
[2,3]
[3,1]
[3,2]
[3,3]

Process finished with exit code 0
1
2
3
4
5
6
7
8
9
10
11

https://www.mathsisfun.com/combinatorics/combinations-permutations.html (opens new window)

← 组合 →