小傅哥 bugstack 虫洞栈

# 《程序员数学：整数拆分》

作者：小傅哥
博客：https://bugstack.cn (opens new window)
源码：https://github.com/fuzhengwei/java-algorithms (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

# 一、前言

4可以被拆分为；3+1、2+2、2+1+1、1+1+1+1，这个过程叫做整数划分，表示在数论和组合学中，正整数n的划分。

那么这东西在数学和计算机科学的领域都有啥用呢；

  • 组合学：配分函数与将集合划分为子集的概念密切相关，在组合学中使用它来计算可以将集合划分为一定大小的子组的方式的数量。
  • 数论：配分函数在数论中用于研究整数的性质及其相互之间的关系。它还用于研究素数的分布。
  • 算法：分区函数可以用来解决各种涉及分区和子集求和问题的问题，例如背包问题和子集​​求和问题。
  • 物理学：配分函数与统计力学的概念有关，用于热力学系统的研究。它还用于研究量子系统的行为。
  • 计算机科学：分区函数在计算机科学中用于解决涉及数据结构的问题，例如哈希表和动态规划。它还用于计算机程序算法的设计。

# 二、分区图示

在维基百科中介绍，有两种常用的图解方法来表示分区：以Norman Macleod Ferrers命名的 Ferrers 图和以Alfred Young命名的 Young 图。两者都有几种可能的约定；在这里，我们使用英文符号，图表在左上角对齐。

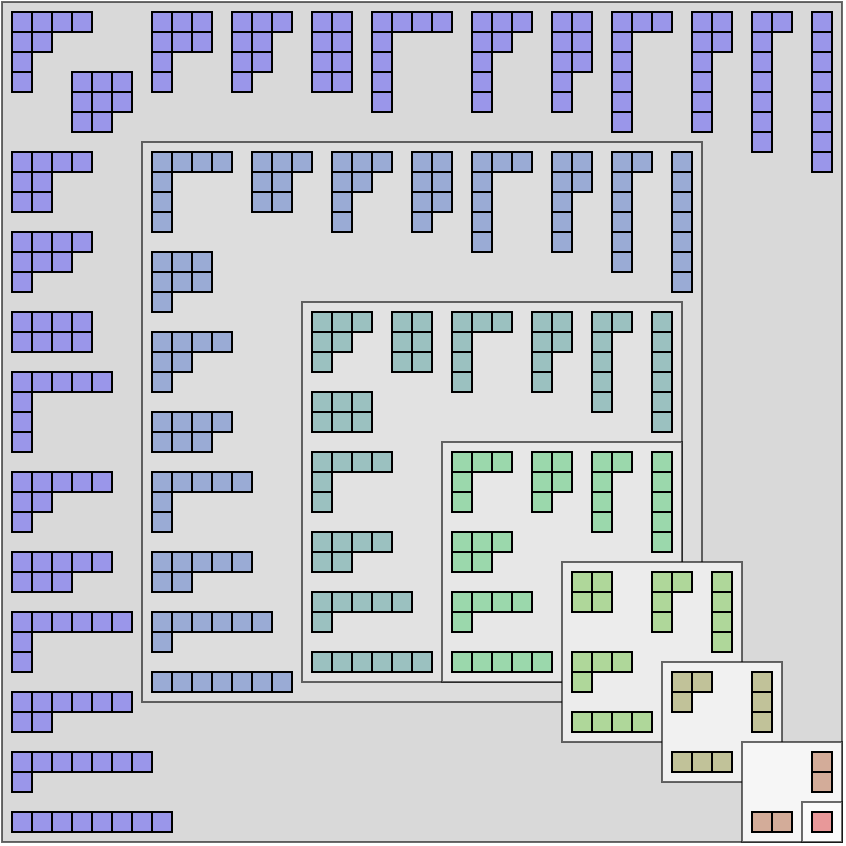
  • 与正整数 1 到 8 的分区相关联的Young 图。它们的排列使得正方形主对角线反射下的图像是共轭分区。

# 三、案例实现

public static int integerPartition(int number) {
    // 创建矩阵
    int[][] partitionMatrix = new int[number + 1][number + 1];
    // 填充数据，需要将数字 1，2，3，...，n 与数字 0 组合的方法数。
    for (int numberIndex = 1; numberIndex <= number; numberIndex++) {
        partitionMatrix[0][numberIndex] = 0;
    }
    // 从 0，0 和 1，0 和 1 和 2，0 和 1 和 2 和 3 等数字中形成数字 0 的方法数。显然，我们只能使用数字 0 本身形成数字 0 的一种方法。
    for (int summandIndex = 0; summandIndex <= number; summandIndex++) {
        partitionMatrix[summandIndex][0] = 1;
    }
    // 通过动态规划方法来探究我们如何从 0，1，...，m 的加数中形成数字 m 的其他可能的选项。
    for (int summandIndex = 1; summandIndex <= number; summandIndex++) {
        for (int numberIndex = 1; numberIndex <= number; numberIndex++) {
            if (summandIndex > numberIndex) {
                // 如果加数大于当前数字本身，那么它就不会增加任何新的数字形成方法。因此，我们可以直接从上面的行中复制数字。
                partitionMatrix[summandIndex][numberIndex] = partitionMatrix[summandIndex - 1][numberIndex];
            } else {
                /*
                 * 组合数等于不使用当前加数形成相同数字的组合数加上使用当前加数形成当前数字减去当前加数的数字的组合数。
                 * 例如，使用 {0, 1, 2} 的加数形成 5 的方法数等于使用 {0, 1} 的加数形成 5 的方法数（排除了加数 2）加上使用 {0, 1, 2} 的加数形成 3 的方法数（包括加数 2）的和。
                 */
                int combosWithoutSummand = partitionMatrix[summandIndex - 1][numberIndex];
                int combosWithSummand = partitionMatrix[summandIndex][numberIndex - summandIndex];
                partitionMatrix[summandIndex][numberIndex] = combosWithoutSummand + combosWithSummand;
            }
        }
    }
    return partitionMatrix[number][number];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
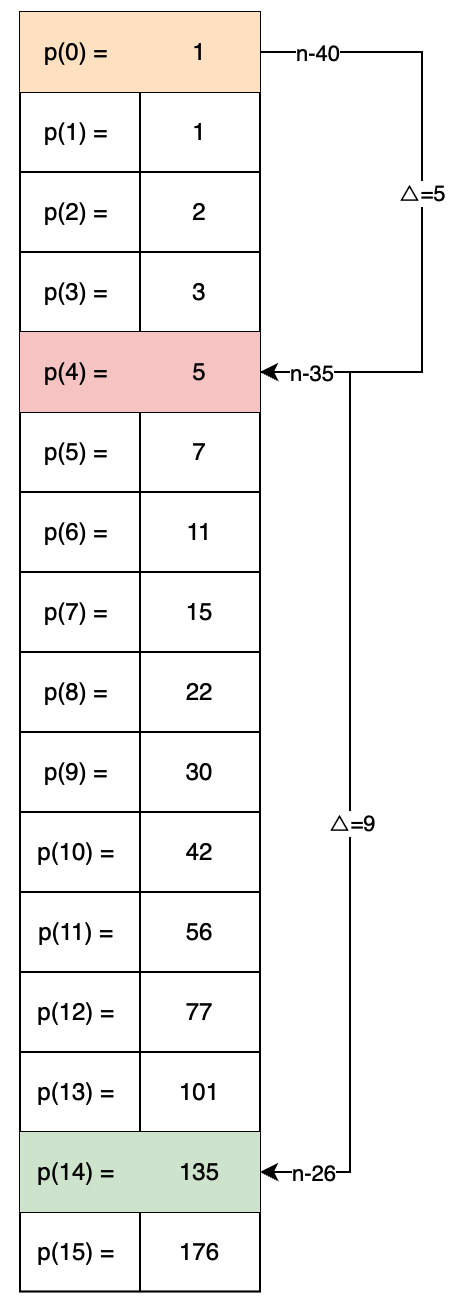
  • 这段代码使用了动态规划来求解数字分割问题。它首先创建了一个 number+1 行 number+1 列的二维数组 partitionMatrix，然后使用三重循环来填充这个数组。
  • 第一重循环从 1 到 number，枚举数字 numberIndex。第二重循环从 0 到 number，枚举数字 summandIndex。第三重循环从 1 到 number，枚举数字 numberIndex。
  • 在这个三重循环中，partitionMatrix[summandIndex][numberIndex] 表示将数字 numberIndex 分割成若干个不大于 summandIndex 的正整数的和的方案数。根据动态规划的思想，这个值可以从 partitionMatrix[summandIndex][numberIndex-summandIndex] 转移而来。这样就可以通过填充这个二维数组来求解数字分割问题。
  • 最后，返回了 partitionMatrix[number][number]，即将数字 number 分割成若干个不大于 number 的正整数的和的方案数。

https://en.wikipedia.org/wiki/Partition_(number_theory) (opens new window)

← 割圆术 LiuHui →