《程序员数学：离散傅立叶变换》—— 把时间信号解析成构成它的频率

作者：小傅哥
博客：https://bugstack.cn (opens new window)
源码：https://github.com/fuzhengwei/java-algorithms (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

一、前言

离散傅立叶变换（DFT）是一种常用的数字信号处理方法，它可以用来将时域信号转换为频域信号，或者将频域信号转换回时域信号。这种变换有许多应用，包括：

• 图像压缩：通过将图像的频谱中的低频分量保留，并删除高频分量来减小图像文件大小。
• 音频信号处理：可以使用DFT来分析和修改音频信号中的频谱特征，例如增强低频或降低高频。
• 时域信号的分析：DFT可以用来确定时域信号中的周期性和波形。
• 将时域信号转换为频域信号以进行信号滤波：可以使用DFT将信号转换为频域，然后使用滤波器来滤除不需要的频率分量，再将信号转换回时域。

这些只是DFT的一些常用用途，实际上还有许多其他用途。

二、离散傅立叶变换

离散傅立叶变换( DFT) 将函数的等间隔样本的有限序列转换为离散时间傅立叶变换 (DTFT) 的等间隔样本的相同长度序列，这是频率的复值函数。DTFT 采样的间隔是输入序列持续时间的倒数。逆 DFT 是一个傅立叶级数，使用 DTFT 样本作为相应 DTFT 频率下的复正弦曲线的系数。它具有与原始输入序列相同的样本值。因此，DFT 被称为原始输入序列的频域表示。如果原始序列跨越函数的所有非零值，则其 DTFT 是连续的（且是周期性的），并且 DFT 提供一个周期的离散样本。如果原始序列是周期函数的一个循环，

离散傅立叶变换变换N复数序列：

{x n } = x 0 , x 1 , x 2 ..., x N-1

进入另一个复数序列：

{X k } = X 0 , X 1 , X 2 ..., X N-1

定义如下：

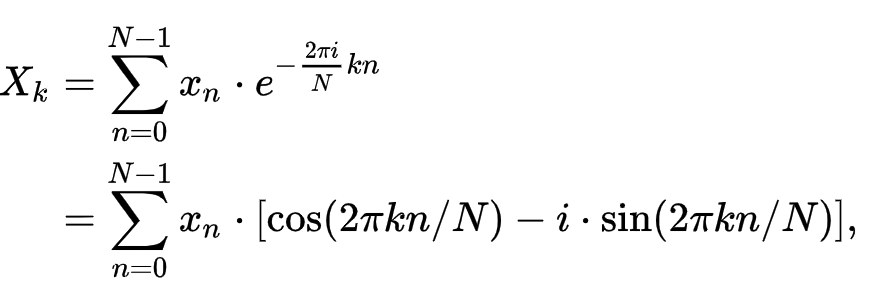
离散时间傅立叶变换( DTFT ) 是傅立叶分析的一种形式，适用于连续函数的均匀间隔样本。术语离散时间是指变换对离散数据（样本）进行操作，其间隔通常具有时间单位。它仅从样本中生成一个频率函数，该函数是原始连续函数的连续傅立叶变换的周期性求和。

快速傅立叶变换( FFT ) 是一种算法，它在一段时间（或空间）内对信号进行采样并将其分成频率分量。这些分量是不同频率的单一正弦振荡，每个都有自己的振幅和相位。

下图说明了此转换。在图中测量的时间段内，信号包含 3 个不同的主频率。

时域和频域中的信号视图：

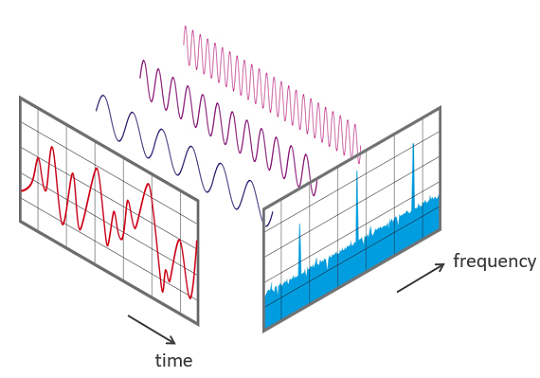
FFT 算法计算序列的离散傅立叶变换 (DFT) 或其逆变换 (IFFT)。傅立叶分析将信号从其原始域转换为频域中的表示，反之亦然。FFT 通过将 DFT 矩阵分解为稀疏（大部分为零）因子的乘积来快速计算此类变换。因此，它设法降低了从 O(n 2 ) 计算 DFT 的复杂性，如果简单地将 DFT 的定义应用到 O(n log n)，就会出现这种复杂性，其中 n 是数据大小。

这里对 10、20、30、40 和 50 Hz 的余弦波之和进行离散傅立叶分析：

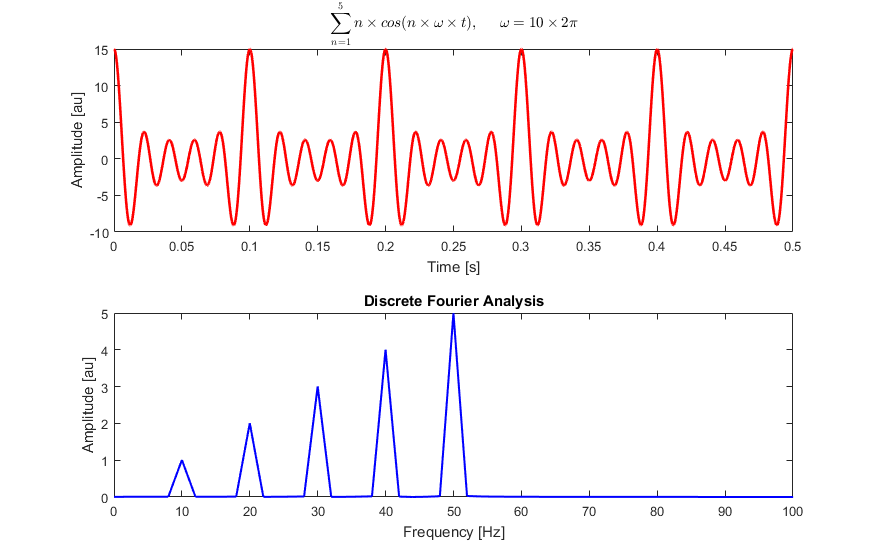
三、解释

傅立叶变换是有史以来最深刻的见解之一。不幸的是，含义隐藏在密集的方程式中：

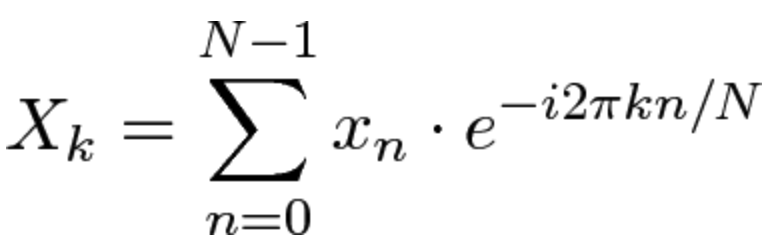
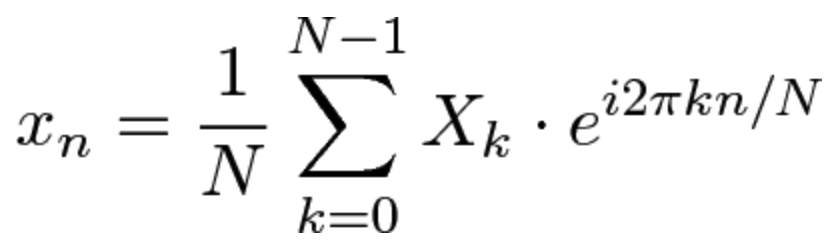
与其跳入符号，不如让我们亲身体验一下关键思想。这是一个通俗易懂的比喻：

• *傅立叶变换有什么作用？*给定一杯冰沙，它会找到食谱。
• *如何？*通过过滤器运行冰沙以提取每种成分。
• *为什么？*食谱比冰沙本身更容易分析、比较和修改。
• *我们如何取回冰沙？*混合成分。

用圆圈思考，而不仅仅是正弦曲线

傅立叶变换是关于圆形路径（不是一维正弦曲线），而欧拉公式是一种生成路径的巧妙方法：

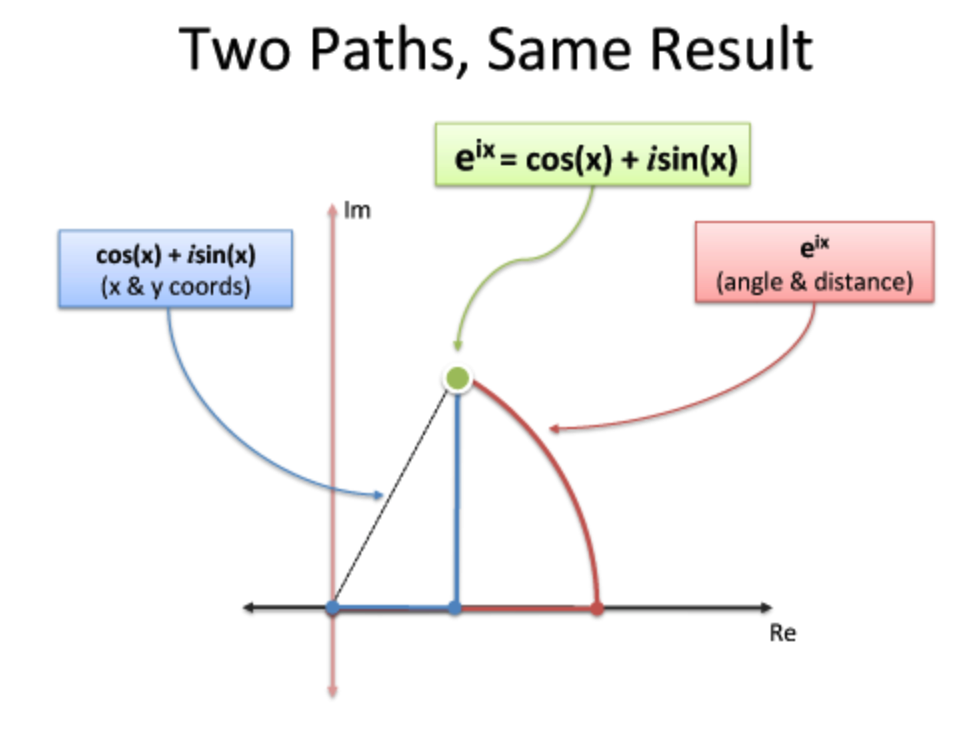
一定要用虚指数绕圈吗？没有。但它方便且紧凑。当然，我们可以将我们的路径描述为二维（真实和虚构）的协调运动，但不要忘记大局：我们只是在绕圈移动。

发现完整的转换

重要见解：我们的信号只是一堆时间尖峰！如果我们合并每个时间尖峰的配方，我们应该得到完整信号的配方。

傅立叶变换逐个频率地构建配方：

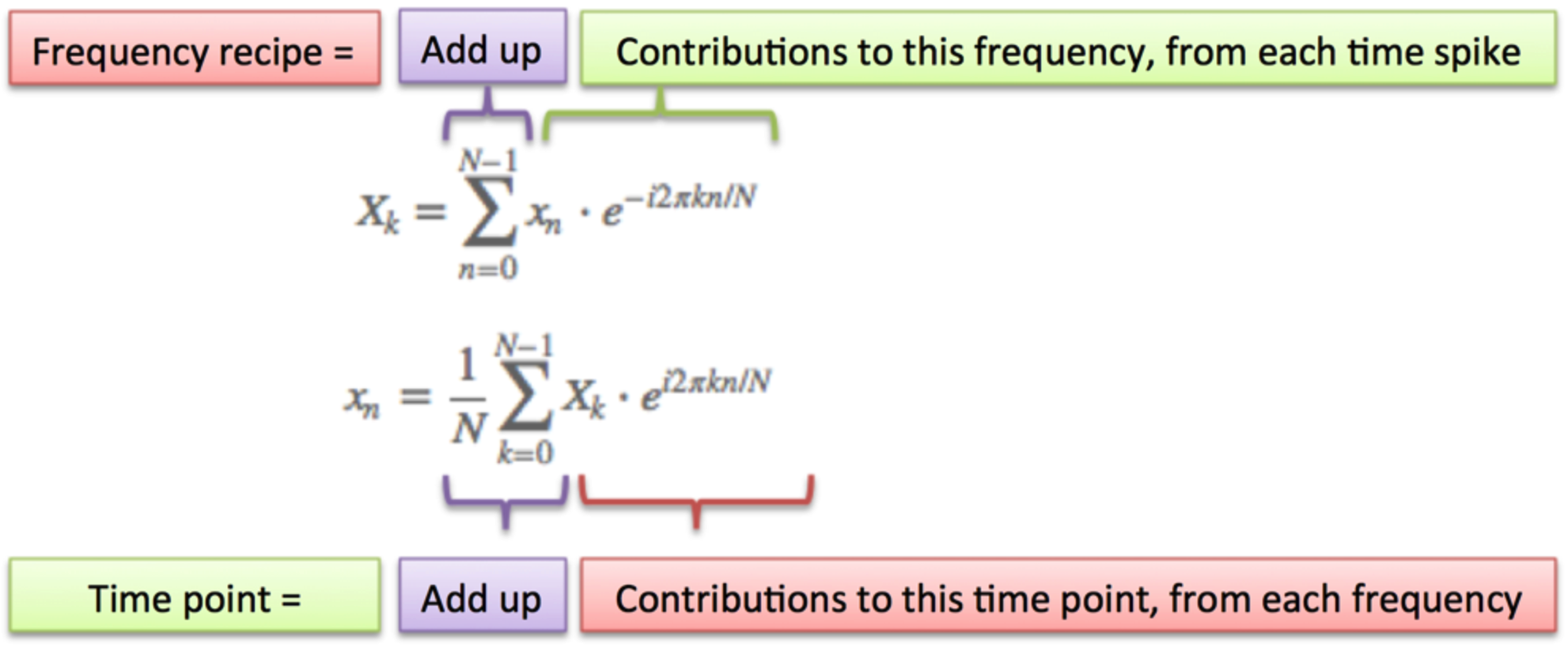
一些注意事项：

• N = 我们拥有的时间样本数
• n = 我们正在考虑的当前样本 (0 ... N-1)
• x n = 时间 n 的信号值
• k = 我们正在考虑的当前频率（0 赫兹到 N-1 赫兹）
• X k = 信号中频率 k 的量（振幅和相位，复数）
• 1/N 因子通常移动到反向变换（从频率回到时间）。这是允许的，尽管我更喜欢正向变换中的 1/N，因为它给出了时间尖峰的实际大小。您可以变得狂野，甚至可以在两个变换上使用 1/sqrt(N)（向前和向后创建 1/N 因子）。
• n/N 是我们经历的时间的百分比。2 _ pi _ k 是以弧度/秒为单位的速度。e^-ix 是我们向后移动的循环路径。对于这个速度和时间，组合就是我们移动了多远。
• 傅立叶变换的原始方程只是说“添加复数”。许多编程语言无法直接处理复数，因此您将所有内容都转换为直角坐标并相加。

Stuart Riffle 对傅立叶变换有很好的解释：

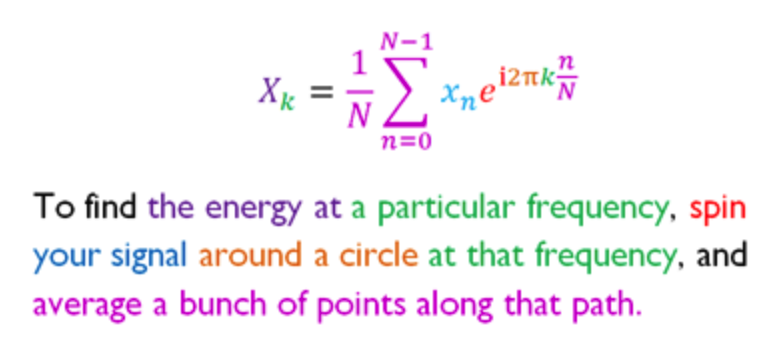
四、实现

1. Apache Math 函数

@Test
public void test_ApacheMath() {
    double[] inputData = null;
    int arrayLength = 4 * 1024;
    inputData = new double[arrayLength];
    for (int index = 0; index < inputData.length; index++) {
        inputData[index] = (Math.random() - 0.5) * 100.0;
    }
    FastFourierTransformer fft = new FastFourierTransformer(DftNormalization.STANDARD);
    Complex[] complexes = fft.transform(inputData, TransformType.FORWARD);
    for (int i = 0; i < 10; i++) {
        System.out.print(inputData[i] + "\t");
        System.out.println(complexes[i]);
    }
}

• 需要引入 commons-math3

2. 基础实现

public Complex[] dft(Complex[] x) {
    int n = x.length;
    // exp(-2i*n*PI)=cos(-2*n*PI)+i*sin(-2*n*PI)=1
    if (n == 1)
        return x;
    Complex[] result = new Complex[n];
    for (int i = 0; i < n; i++) {
        result[i] = new Complex(0, 0);
        for (int k = 0; k < n; k++) {
            //使用欧拉公式e^(-i*2pi*k/N) = cos(-2pi*k/N) + i*sin(-2pi*k/N)
            double p = -2 * k * Math.PI / n;
            Complex m = new Complex(Math.cos(p), Math.sin(p));
            result[i].plus(x[k].multiple(m));
        }
    }
    return result;
}

3. 快速实现

public Complex[] fft(Complex[] x) {
    int n = x.length;
    // 因为exp(-2i*n*PI)=1，n=1时递归原点
    if (n == 1) {
        return x;
    }
    // 如果信号数为奇数，使用dft计算
    if (n % 2 != 0) {
        return dft(x);
    }
    // 提取下标为偶数的原始信号值进行递归fft计算
    Complex[] even = new Complex[n / 2];
    for (int k = 0; k < n / 2; k++) {
        even[k] = x[2 * k];
    }
    Complex[] evenValue = fft(even);
    // 提取下标为奇数的原始信号值进行fft计算
    // 节约内存
    for (int k = 0; k < n / 2; k++) {
        even[k] = x[2 * k + 1];
    }
    Complex[] oddValue = fft(even);
    // 偶数+奇数
    Complex[] result = new Complex[n];
    for (int k = 0; k < n / 2; k++) {
        // 使用欧拉公式e^(-i*2pi*k/N) = cos(-2pi*k/N) + i*sin(-2pi*k/N)
        double p = -2 * k * Math.PI / n;
        Complex m = new Complex(Math.cos(p), Math.sin(p));
        result[k] = evenValue[k].plus(m.multiple(oddValue[k]));
        // exp(-2*(k+n/2)*PI/n) 相当于 -exp(-2*k*PI/n)，其中exp(-n*PI)=-1(欧拉公式);
        result[k + n / 2] = evenValue[k].minus(m.multiple(oddValue[k]));
    }
    return result;
}

public Complex[] dft(Complex[] x) {
    int n = x.length;
    // 1个信号exp(-2i*n*PI)=1
    if (n == 1)
        return x;
    Complex[] result = new Complex[n];
    for (int i = 0; i < n; i++) {
        result[i] = new Complex(0, 0);
        for (int k = 0; k < n; k++) {
            //使用欧拉公式e^(-i*2pi*k/N) = cos(-2pi*k/N) + i*sin(-2pi*k/N)
            double p = -2 * k * Math.PI / n;
            Complex m = new Complex(Math.cos(p), Math.sin(p));
            result[i].plus(x[k].multiple(m));
        }
    }
    return result;
}

---

本文来自于对Github文章的翻译：https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fourier-transform (opens new window) 如果你还需要更多的资料可以阅读一下内容；

• 傅里叶变换交互式指南 (opens new window)
• Better Explained YouTube 上的 DFT (opens new window)
• 3Blue1Brown 在 YouTube 上发布的英国《金融时报》 (opens new window)
• YouTube 上的 FFT，作者：Simon Xu (opens new window)
• 维基百科
  • 金融时报 (opens new window)
  • 离散傅里叶变换 (opens new window)
  • 双频傅立叶变换 (opens new window)
  • 快速傅里叶变换 (opens new window)