《程序员数学：笛卡尔积》- 多集合结果

作者：小傅哥
博客：https://bugstack.cn (opens new window)
源码：https://github.com/fuzhengwei/java-algorithms (opens new window)

沉淀、分享、成长，让自己和他人都能有所收获！😄

一、前言

在集合论中，笛卡尔积是一种数学运算，它从多个集合中返回一个集合（或乘积集或简单的乘积）。也就是说，对于集合 A 和 B，笛卡尔积 A × B 是所有有序对 (a, b) 的集合，其中 a ∈ A 和 b ∈ B。

它把每个集合中的元素看作一维，并组合成多维的矩阵。例如，假设有两个集合A和B，其中A = {a1, a2}，B = {b1, b2}，那么笛卡尔积就是：A x B = {(a1, b1), (a1, b2), (a2, b1), (a2, b2)}。笛卡尔积可以用来解决许多数学问题，也可以用于编程和计算机科学中。

二、扑克牌场景

一副扑克牌有52张，13种数字和4种花色组成。其实这就是一个笛卡尔积的体现。

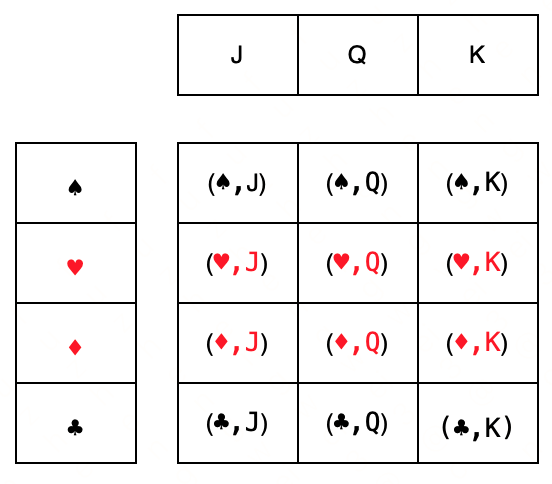
标准扑克牌 {A , K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2} 形成一个 13 元素集。牌套{♠, ♥ , ♦ , ♣}形成一个四元素集。这些集合的笛卡尔积返回一个包含 52 个有序对的 52 元素集合，对应于所有 52 张可能的扑克牌。

Ranks × Suits 返回 {(A, ♠), (A, ♥ ), (A, ♦ ), (A, ♣), (K, ♠), …, (3, ♣), (2 , ♠), (2, ♥ ), (2, ♦ ), (2, ♣)}。

Suits × Ranks 返回一组形式 {(♠, A), (♠, K), (♠, Q), (♠, J), (♠, 10), …, (♣, 6), (♣ , 5), (♣, 4), (♣, 3), (♣, 2)}。

这两个集合是不同的，甚至是不相交的，但是它们之间存在一个自然的双射，在该双射下，(3, ♣) 对应于 (♣, 3) 等等。

三、实现笛卡尔积

public class CartesianProduct {

    public static List<List<Object>> cartesianProduct(List<Object> setA, List<Object> setB) {
        // Check if input sets are not empty.
        // Otherwise return null since we can't generate Cartesian Product out of them.
        if (setA == null || setB == null || setA.isEmpty() || setB.isEmpty()) {
            return null;
        }

        // Init product set.
        List<List<Object>> product = new ArrayList<>();

        // Now, let's go through all elements of a first and second set and form all possible pairs.
        for (Object elementA : setA) {
            for (Object elementB : setB) {
                // Add current product pair to the product set.
                List<Object> currentPair = new ArrayList<>();
                currentPair.add(elementA);
                currentPair.add(elementB);
                product.add(currentPair);
            }
        }

        // Return cartesian product set.
        return product;
    }

}

该方法的参数是两个列表："setA" 和 "setB"。在方法开始处，它检查了两个列表是否为空，如果任意一个列表为空，则返回空值（null）。

如果两个列表都不为空，则在内部循环中计算两个列表的笛卡尔积：第一个循环遍历第一个列表，第二个循环遍历第二个列表。两个循环的每次迭代都会生成一个当前的产品对，该产品对由两个元素组成：一个元素是第一个列表的当前元素，另一个元素是第二个列表的当前元素。这个产品对存储在 "product" 列表中，并在循环结束时返回。

因此，该方法将两个列表的笛卡尔积作为一个列表中的产品对返回。

---

• 笛卡尔积 (opens new window)