# 《程序员数学:割圆术》—— 基于 N-gons 的近似 π 计算
作者:小傅哥
博客:https://bugstack.cn (opens new window)
源码:https://github.com/fuzhengwei/java-algorithms (opens new window)
沉淀、分享、成长,让自己和他人都能有所收获!😄
# 一、前言
割圆术的历史
刘徽的π算法是由曹魏国的数学家刘徽(公元3世纪)发明的。在他之前,圆的周长与直径之比在中国常被实验取为3.0,而张衡(78-139)则将其定为3.1724(根据天球与地球直径的比例) , 92/29 ) 或作为 π ≈ √10 ≈ 3.162 但 刘辉对这个数值并不满意,评论说它太大了,超出了标准。
另一位数学家王凡(219–257) 给出了π ≈ 142/45 ≈ 3.156。所有这些经验π值都精确到两位数(即小数点后一位)。刘徽是第一位提供精确计算π的严格算法的中国数学家。刘辉自己用九十六边形计算,精度达到五位数:π≈3.1416。
# 二、刘辉算法
刘徽从一个六边形开始。设是六边形M一侧的长度,是圆的半径。AB``r
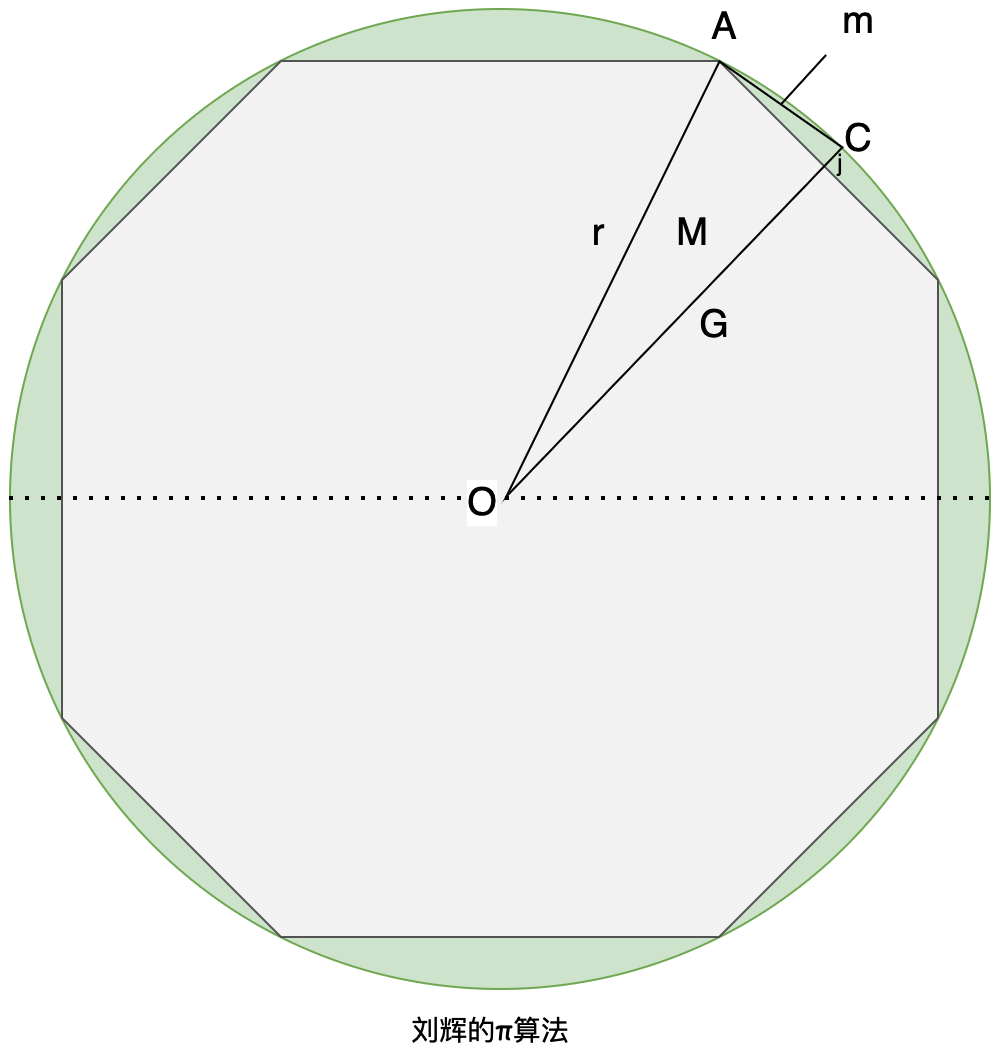
AB用线平分OPC,AC成为十二边形(12 边形)的一侧,令其长度为m。让 be 的长度和bePC的j长度。`OP``G
AOP,APC是两个直角三角形。刘徽反复引用勾股定理 (opens new window)(勾股定理):
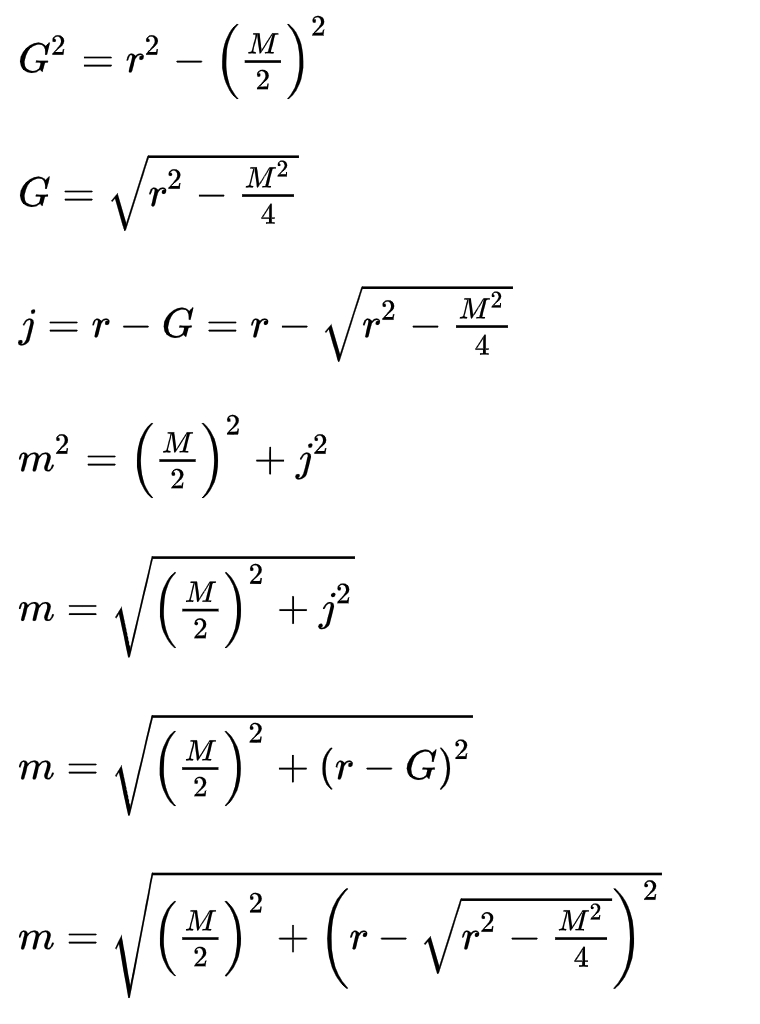
从这里开始,现在有一种从 确定的技术m,M它给出了具有两倍边数的多边形的边长。从六边形开始,刘辉可以用这个公式计算出十二边形的边长。然后在给定十二边形的边长的情况下继续重复确定 24 边形的边长。他可以根据需要递归多次执行此操作。知道了如何确定这些多边形的面积,刘辉就可以进行近似了π。
# 三、算法实现
直到去测试验证割圆术我才体会到为啥要用那么多强大的计算机来计算π了,因为像我这样的电脑根本计算不出多少位π值,就把风扇🏃🏻的嗖嗖的了!
# 1. 复杂度高
public static double liuHui01(int splitPoint) {
// 圆的半径
double r = 1.0;
// 正方形的边长
double s = 2.0 * r;
Random rand = new Random();
// 计算圆内随机生成的点的个数
int m = 0;
for (int i = 0; i < splitPoint; i++) {
double x = rand.nextDouble() * s - r;
double y = rand.nextDouble() * s - r;
if (x * x + y * y <= r * r) {
m++;
}
}
// 面积比 = 圆的面积 / 正方形的面积
double p = (double) m / splitPoint;
// 圆周率 = 面积比 * 4
return p * 4;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- liuHui01使用了一个叫做重心法的算法,将圆划分成若干个小正方形,然后在每个小正方形内随机生成点,最后统计出有多少个点在圆内。
- 这个方法接收一个整数 splitPoint,表示圆内划分的小正方形的个数。它首先声明了一个叫做 r 的常量,表示圆的半径,然后计算出正方形的边长。然后,它创建了一个随机数生成器 rand,并循环 splitPoint 次,每次生成一个随机数对 (x, y),表示在某个小正方形内的点的坐标。接着,它判断这个点是否在圆内,如果是,就将计数器 m 加 1。
- 最后,它计算出圆内的点的占比,并将这个占比乘以 4,得到圆周率的近似值。
# 2. 复杂度低
static double getNGonSideLength(double sideLength, int splitCounter) {
if (splitCounter <= 0) {
return sideLength;
}
double halfSide = sideLength / 2;
// 使用勾股定理(勾股定理)
double perpendicular = Math.sqrt(Math.pow(circleRadius, 2) - Math.pow(halfSide, 2));
double excessRadius = circleRadius - perpendicular;
double splitSideLength = Math.sqrt(Math.pow(excessRadius, 2) + Math.pow(halfSide, 2));
return getNGonSideLength(splitSideLength, splitCounter - 1);
}
static int getNGonSideCount(int splitCount) {
// 内接六边形 (6-gon) 开始
int hexagonSidesCount = 6;
// 在每次拆分迭代中,我们制作 N 边形:6 边形、12 边形、24 边形、48 边形等等。
return hexagonSidesCount * (splitCount > 0 ? (int) Math.pow(2, splitCount) : 1);
}
public static double liuHui02(int splitCount) {
double nGonSideLength = getNGonSideLength(circleRadius, splitCount - 1);
int nGonSideCount = getNGonSideCount(splitCount - 1);
double nGonPerimeter = nGonSideLength * nGonSideCount;
double approximateCircleArea = (nGonPerimeter / 2) * circleRadius;
return approximateCircleArea / Math.pow(circleRadius, 2);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
- 方法 liuHui02 接收一个整数 splitCount,它表示圆内进行的拆分次数。在内部,这个方法调用了两个静态方法 getNGonSideLength 和 getNGonSideCount,分别用来计算所得多边形的边长和边数。然后,它使用这些值计算出多边形的周长,并利用这个周长来估算出圆的面积。最后,它返回圆的面积与多边形的面积之比。
- 静态方法 getNGonSideLength 递归地使用勾股定理来计算所得多边形的边长。这个方法的第一个参数是边长,第二个参数是拆分次数,在拆分次数不为正数时递归终止,并返回边长。否则,它会将边长分成两半,并使用勾股定理计算出所得多边形的新边长。然后,它会使用新边长继续进行递归,直到拆分次数变成正数为止。
- 静态方法 getNGonSideCount 使用与 splitCount 相关的算法来计算所得多边形的边数。在这个方法内,有一个常量 hexagonSidesCount 被初始化为 6,表示一个内接的 6 边形。然后,它会根据 splitCount 的值来进行计算。如果 splitCount 是正数,那么它会返回 hexagonSidesCount 乘以 2 的 splitCount 次方,否则就返回 hexagonSidesCount 本身。这个方法的返回值就是所得多边形的边数。
- 综上所述,这段代码通过计算内接的多边形的边长和边数,并使用这些信息估算圆的面积,最后计算圆的面积与多边形的面积之比。
https://en.wikipedia.org/wiki/Liu_Hui%27s_%CF%80_algorithm (opens new window)

