野路子搞算法《两数之和》，带着小白刷面试算法题

Github： https://github.com/MyGitBooks/niubility-algorithm
本文档是作者小傅哥通过从leetcode 剑指offer 编程之美 等资料中收集算法题目并加以逻辑分析和编码搞定题目，最终编写资料到本文档中，为大家提供在算法领域的帮助。如果本文能为您提供帮助，请给予支持(加入、点赞、分享)！

一、前言

在这之前我基本没怎么关注过leetcode，还是最近有人经常说面试刷题，算法刷到谷歌上班去了。我才开始了解下，仔细一看原来虽然没关注过，但是类似的题还是做过的并且还买过一本《编程之美》的书。

在 leetcode-cn.com (opens new window) 中每个算法题都有编号；1 2 3 ... 1566，而且还在增加。你我都是新人，既然没了解过那就从第一题开始吧，尝试从算法中吸取一些创新的思路。否则为什么那么多公司面试招聘都会去考下算法！谷歌 字节跳动 腾讯 阿里 等等

对于这个算法题来说我还是蛮喜欢的，因为我是属于那种很偏科的男人，通常数学：140分，英语：40分(当年)。好！理由找好了，开始刷个题。听说数学好的男人都不简单！ 所以我打算接下来定期的做一些算法题，同时将我的思路进行整理，写成笔记分享给新人，一起从算法中成长。

二、时间复杂度

时间复杂度可以说是算法的基础，如果不在乎时间复杂度，那么没有 for 循环解决不了问题！而我们一般所说的时间复杂度以及耗时排列包括；O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n) 等。那么一段代码的耗时主要由各个行为块的执行次数相加并去掉最小影响系数而得出的，接下来先看下这种东西是如何计算出来的。

1. O(n)

代码块

int n = 10;
for (int i = 0; i < n; i++) {
    System.out.println(i);
}

序号	代码块	耗时
1	int n = 10	1
2	int i = 0	1
3	i < n	n + 1
4	i++	n
5	System.out.println(i)	n

最终耗时：

sum = 1 + 1 + n + 1+ n + n
	= 3n+3
	= n (忽略低阶梯)

---

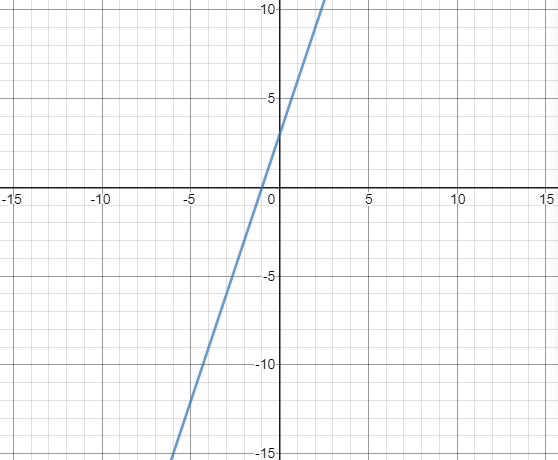
从公式和象限图中可以看到，当我们的公式3n+3，随着 n 的数值越来越大的时候，常数3就可以忽略低阶梯不记了。所以在这段代码中的时间复杂度就是；O(n)

所谓低阶项，简单地说就是当n非常大时，这个项相对于另外一个项很小，可以忽略，比如n相对于n^2,n就是低阶项

2. O(logn)

代码块

int sum = 1, n = 10;
while (sum < n) {
    sum = sum * 2;
}

最终耗时：

这回我们只看执行次数最多的，很明显这是一个 2 * 2 * 2 ··· n，大于 n 跳出循环。 那么我们使用函数；2^x = n，x = logn，就可以表示出整体的时间复杂度为 O(logn)

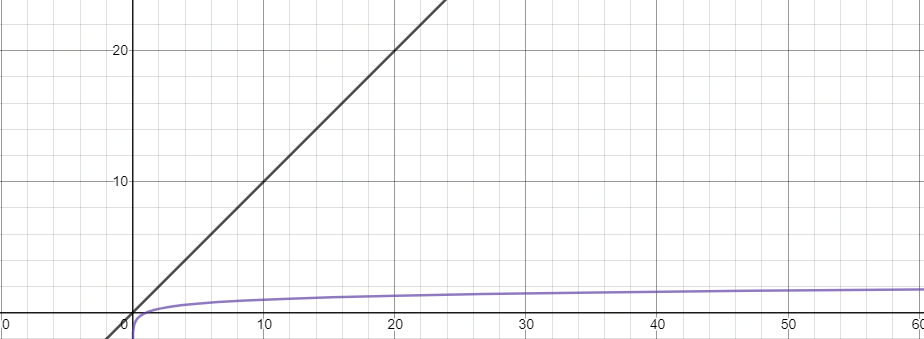
好！结合这两个例子，相信你对时间复杂度已经有所理解，后面的算法题中就可以知道自己的算法是否好坏。

三、算法题：两数之和

https://leetcode-cn.com/problems/two-sum/submissions/ (opens new window)

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9
 
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

java

class Solution {
    public int[] twoSum(int[] nums, int target) {
		// todo
    }
}

四、解题

这是leetcode的第一题，难度简单，其实如果要是使用两层for循环嵌套，确实不太难。但是如果想打败99%的选手还是需要斟酌斟酌算法。

思路1，双层循环

先不考虑时间复杂度的话，最直接的就是双层for循环，用每一个数和数组中其他数做家和比对，如下；

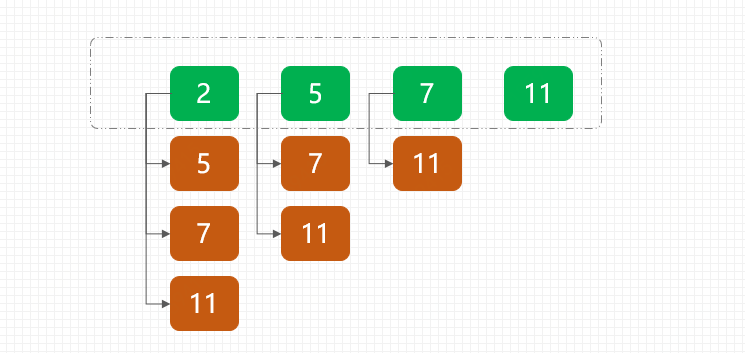
可以看到这样的时间复杂度是；n*(n-1) ··· 43、42、4*1，也就是O(n!)，有点像九九乘法表的结构。

代码：

public int[] twoSum(int[] nums, int target) {
    int[] idxs = new int[2];
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[i] + nums[j] == target) {
                idxs[0] = i;
                idxs[1] = j;
            }
        }
    }
    return idxs;
}

耗时：

• 对于这样的算法虽然能解决问题，但是并不能满足我们的需求，毕竟这个级别的时间复杂度下实在是太慢了。

思路2，单层循环

为了把这样一个双层循环简化为单层，我们最能直接想到的就事放到 Map 这样的数据结构中，方便我们存取比对。那么这样的一个计算过程如下图；

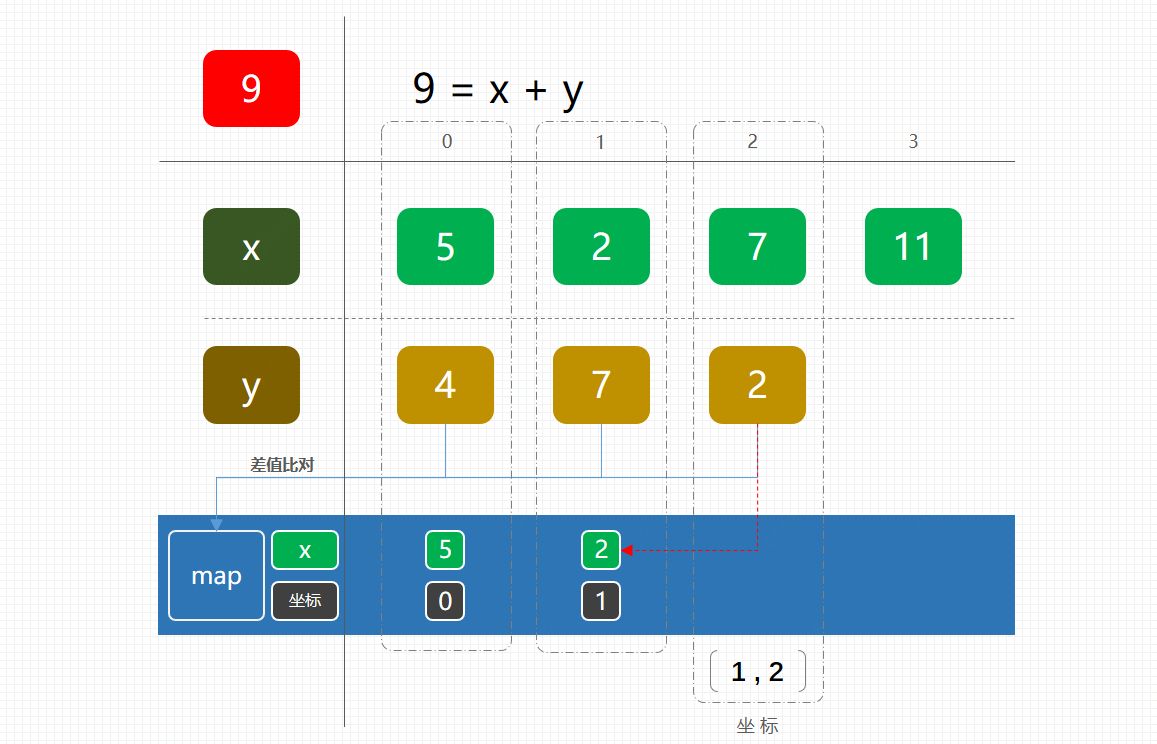
• 这个过程的核心内容是将原来的两数之和改成差值计算，并将每次的差与 Map 中元素进行比对。如果差值正好存在 Map 中，那么直接取出。否则将数存入到 Map 中，继续执行。
• 这个过程就可以将原来的双层循环改为单层，时间复杂度也到了 O(n) 级别。

代码：

public static int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> hashMap = new HashMap<Integer, Integer>(nums.length);
    for (int i = 0; i < nums.length; i++) {
        if (hashMap.containsKey(target - nums[i])) {
            return new int[]{hashMap.get(target - nums[i]), i};
        }
        hashMap.put(nums[i], i);
    }
    return new int[]{-1, -1};
}

耗时：

• 可以看到当我们使用 Map 结构的时候，整个执行执行用时已经有了很大的改善。但是你有考虑过containsKey 与 get 是否为 null 相比哪个快吗？
• 这个算法已经很良好了，但是这个对 key 值的比对还是很耗时的，需要反复的对 map 进行操作，那么我们还需要再优化一下。

思路3，Bit结构

如果说想把我们上面使用 Map 结构的地方优化掉，我们可以考虑下 Map 数据是如何存放的，他有一种算法是自身扩容 2^n - 1 & 元素，求地址。之后按照地址在进行存放数据。那么我们可以把这部分算法拿出来，我们自己设计一个数组结构，将元素进行与运算存放到我们自己定义的数组中。如下图；

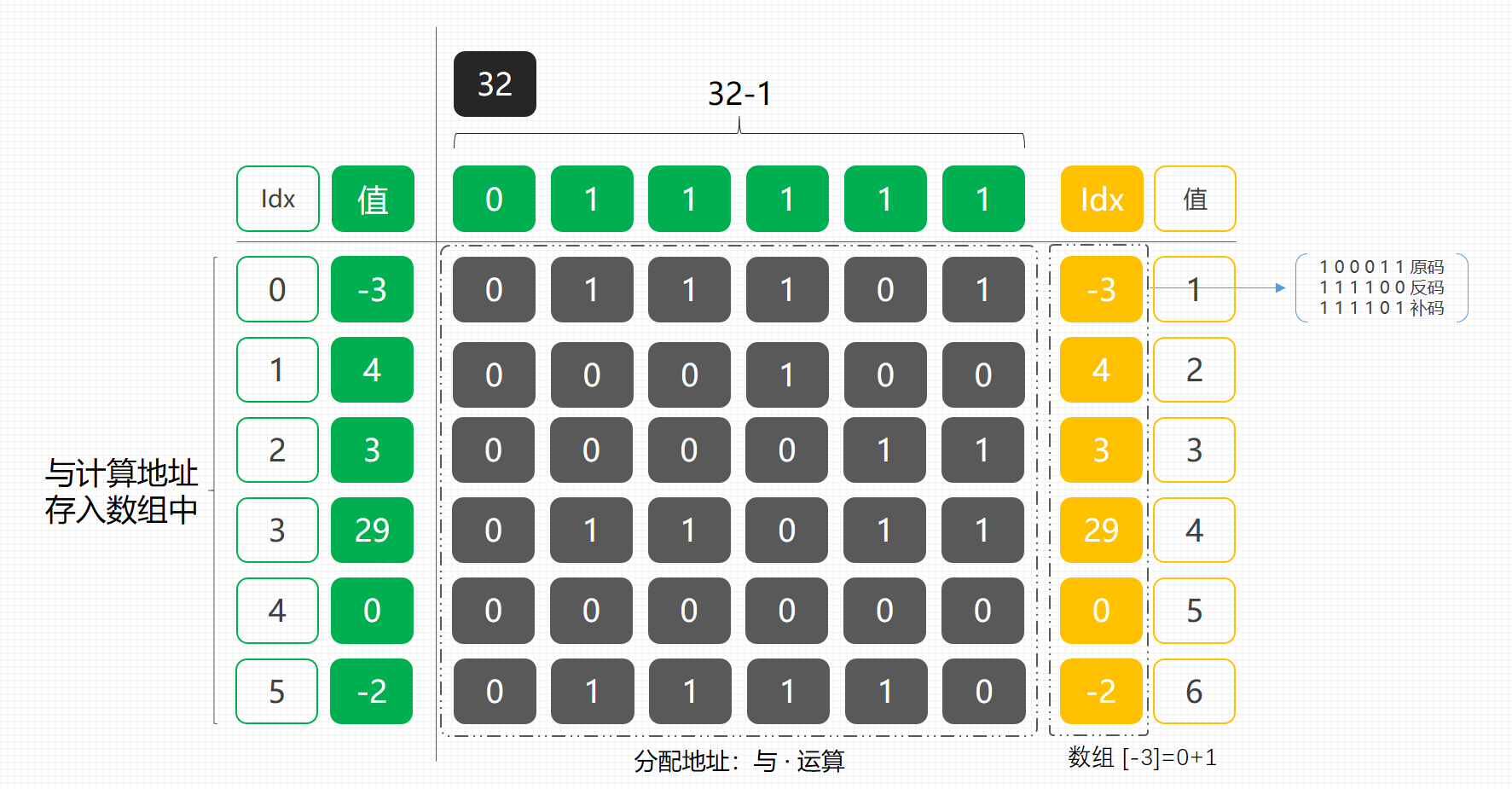
• 左侧是我们假定的入参int[] nums，32是我们设定的值，这个值的设定需要满足存放大小够用，否则地址会混乱。
• 接下来我们使用 32 - 1，也就是二进制 011111与每一个数组中的值进行与运算，求存放地址。
• 当算好地址后，将元素存放在数组中，设置值。这个值就是我们的元素本身位置了，但是需要+1，因为默认数组是0，如果不加1，就看不到位置了。最终使用的时候，可以再将位置结果 -1。

代码：

public static int[] towSum(int[] nums, int target) {
    int volume = 2048;              
    int bitMode = volume - 1;       
    int[] t = new int[volume];      
    for (int i = 0; i < nums.length; i++) {
        int c = (target - nums[i]) & bitMode;
        if (t[c] != 0) return new int[]{t[c] - 1, i};
        t[nums[i] & bitMode] = i + 1;
    }
    return new int[]{-1, -1};
}

• 这个2048是我们试出来的，主要根据leetcode中的单测用例决定。

耗时：

• 出现0毫秒耗时，100%击败，这个不一定每次都这样，可能你试的时候不一样。得益于数据结构的优化使得这个算法的耗时很少。

五、总结

• 野路子搞算法，没有看过算法导论、也没有套用模板，但如果需要后续的不断的加深自己的知识点，也是需要学习的。目前在我看来这些更像是数学题，主要可以提升对同一件事情的多种处理方式，同时也增加个人的编程能力。
• 算法的学习也不太应该套用各种理论，当然每个人看法不一样，我允许你的观点，也要接受我的想法。
• 在各个大厂面试过程中，都有；算法、源码、项目、技术栈以及个人的一些优点，如果你能在前两个点上给面试官很好的印象，那么你就放心的要工资吧。
• 从这篇文章开始，我会陆续做一做算法题，提升自己的功夫底子，也分析给小白。欢迎小白跟随！Git地址：https://github.com/MyGitBooks/niubility-algorithm (opens new window)